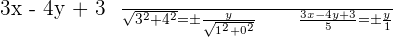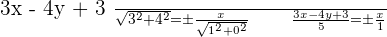Chapters

What is Locus?
A locus is a set of points that satisfy a certain condition or criteria. The area surrounded by loci (which is the plural of locus) is known as region. The concept of Locus was born in the 20th century when mathematicians started to consider a set of points that satisfy a certain condition instead of considering geometric shapes as an entity where you can find points. One of the most frequently asked questions is that what kind of condition or criteria does locus require? Honestly, it could be any mathematical equation. It could be a shape or some kind of curve but this shouldn't be your concern, the most important point is that the set of points should satisfy a particular equation. Those sets of points can be in any form such as coordinates, points, lines, etc. All geometric shapes are defined by locus as a set of points.
Locus has some big applications in the real world. For example, you must have heard the word, "location", do you know the origin of this word? The word "location" is derived from the word locus. Let's compare the word "locus" with the word "location". Since locus is a set of points that satisfy a condition that means we can say that locus represents a position of a certain object. The place where the object is situated or maybe moving is, basically, described by locus. For example, my home has become a locus opposite the cricket stadium.
The criteria that define the locus have to be translated to an algebraic language in order to solve problems involving types of a locus.
Examples of Locus
Here we got some examples of locus
Perpendicular Bisector
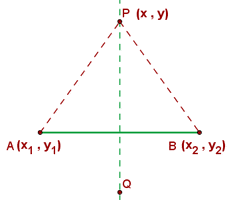
The perpendicular bisector of a line segment is the locus of points on the plane that are equidistant from the endpoints.

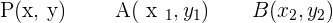
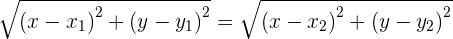
Example
Find the equation of the perpendicular bisector of the line segment with endpoints 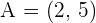 and
and  .
.

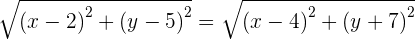


Angle Bisectors
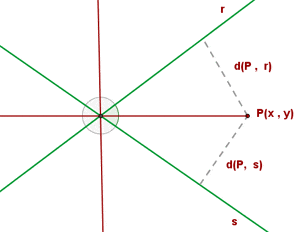
The bisector of an angle is the locus of points on the plane that are equidistant from the rays that form the angle.


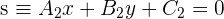

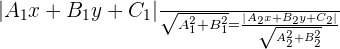
The two angle bisectors are perpendicular between themselves.
Example
Find the equations of the angle bisectors which determine the lines  and
and  .
.


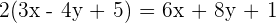
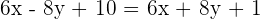
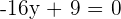
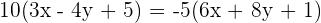

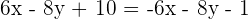
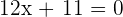
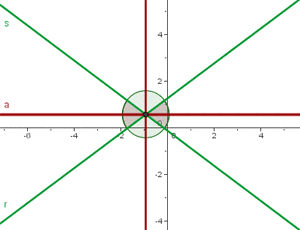
Find the equations of the angle bisectors that form the line 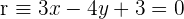 with the coordinate axes.
with the coordinate axes.