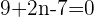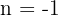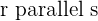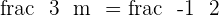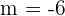Mathematicians suggested that if they categorized lines, this will make our work easier and that is why there are many types of lines such as perpendicular lines, intersecting lines, linear lines, and many more. One of them is parallel lines, so what is a parallel line? If two lines are identical to each other but they never meet and they a distant apart are called parallel lines. Check the below example:
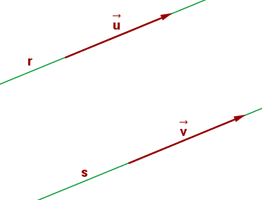
There are two lines, we denoted them with line "r" and line "s". As you can see, both lines have the same direction which means that both lines will never meet each other. In addition, they are a distance apart hence we can call both lines parallel. In conclusion, there are two conditions for parallel lines, the first one is that they will not intersect each other at any point and the second one is that they will be a distance apart. If both conditions are true then only you can call lines parallel. Parallel lines don't exist in only two lines but it can exist in more than two lines.

Pairs of Angles
Imagine two parallel lines and a line intersecting both lines. We also have an image to give you a good picture:
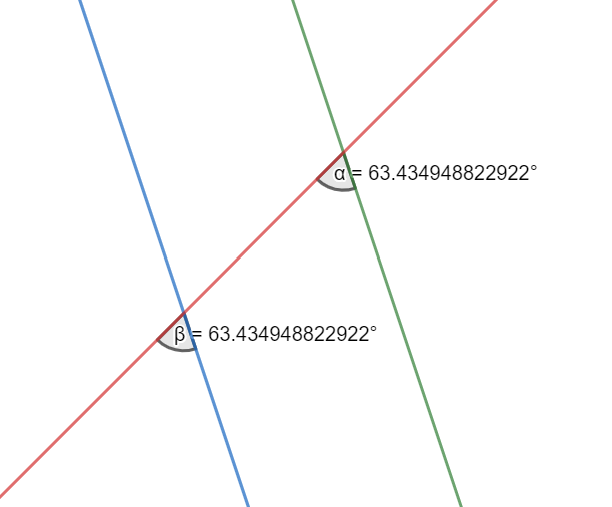
The angle created by the intersecting line will be equal in both parallel but on the same side. If you check the blue line, the angle created by the red line is on the same side of the green line and they both will be equal. In the above image, angle 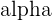 will always be equal to angle
will always be equal to angle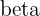 and in the above scenario, the angle is
and in the above scenario, the angle is 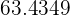 °. In fact, their (talking about
°. In fact, their (talking about 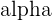 &
& 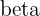 ) opposite angle will be equal which means they will be
) opposite angle will be equal which means they will be 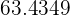 °.
°.
Slope and Equation of a Line
However, the angle isn't the only thing common between parallel lines, there are a few more things through which you can verify that the lines are either parallel or not? One of those things is through the slope. Remember, parallel lines always have the same direction and slope is the change in ordinate per change in abscissa which also shows the direction of the specific line. Since parallel lines have the same direction that means they will have the same slope as well. Hence we can conclude that 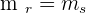
Not only gradient will be similar but the equation of the lines will also be similar. However, the equation can never be equal but it can be similar. Let's take the above example again and find the equation of both parallel lines. The equation of the blue line is  and the equation of the green line is
and the equation of the green line is 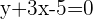 , did you notice something? The x, as well as y components, are the same but the constant is different. That constant is the y-intercept which is the distance between both parallel lines. Therefore, we can conclude that the x and y component of the equation will be the same but the y-intercept will be changed. In short, Two lines are parallel if the respective coefficients of x and y are proportional.
, did you notice something? The x, as well as y components, are the same but the constant is different. That constant is the y-intercept which is the distance between both parallel lines. Therefore, we can conclude that the x and y component of the equation will be the same but the y-intercept will be changed. In short, Two lines are parallel if the respective coefficients of x and y are proportional. 
Vectors and Angle Between Both Lines
In addition, you can find whether the lines are parallel or not with the help of vectors. Two lines are parallel if their directional vectors are equal. 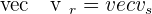 . Last but not least, the angle between both parallel lines will be equal to zero. The reason is pretty simple, these lines don't meet each other at any point, hence the angle between both lines will be equal to zero.
. Last but not least, the angle between both parallel lines will be equal to zero. The reason is pretty simple, these lines don't meet each other at any point, hence the angle between both lines will be equal to zero.
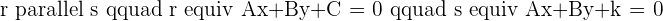

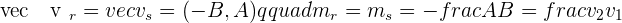
Example
Find the value of k if lines 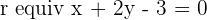 and
and 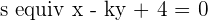 are parallel.
are parallel.
Since both lines are parallel, we can equate both gradients and find the value of k.
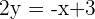
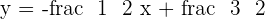

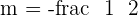







Determine the equation for the line parallel to 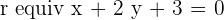 that passes through the point
that passes through the point  .
.
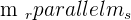
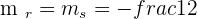
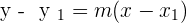



Determine the equation for the line parallel to 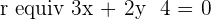 that passes through the point
that passes through the point 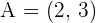 .
.
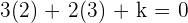
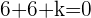

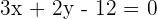
The line  passes through the point
passes through the point  and is parallel to the line
and is parallel to the line  . Calculate the values of m and n.
. Calculate the values of m and n.