When two lines intersect each other, they create a small angle between them. In addition, you don't even need another line, if the line intersects the axis, it still creates an angle from the axis. The angle between two lines is the smaller of the angles formed by the intersection of the two lines The angle can be obtained from:
Derivation of the Formula to Measure Angle
.
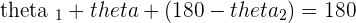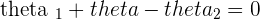
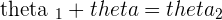
Subtracting
from both sides:
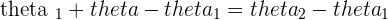
Using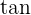
on both sides:
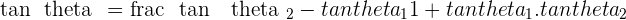
Since you all know that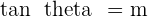
, that means
and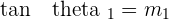
:
Hence, the final formula will be:
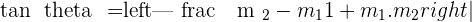
We used the modulus so that the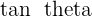
is always equal to a positive number.
Formulas
To find the slope, you need to use this formula:
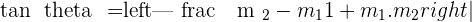
To find their direction vectors: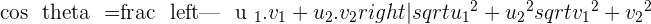
Examples
Find the angle between the lines r and s, if their directional vectors are: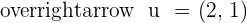
and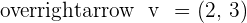
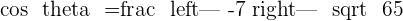
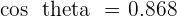
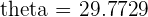° Given the lines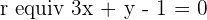
and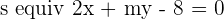
, calculate the value of m so that the two lines form an angle of
°.
°
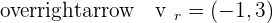
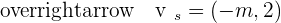
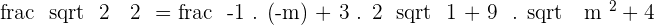
Taking square on both sides:
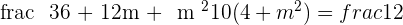
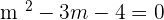
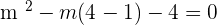
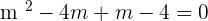
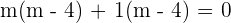
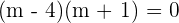
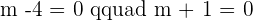
Summarise with AI:
Did you like this article? Rate it!
Loading...
