Chapters

What is a Slope of a Line?
You might be wondering why do we need to find slope in coordinate geometry? Because it finds us different sets of data. For better clarification, we have an example, imagine a distance-time graph. The slope of the graph will tell you the speed of the object. That is just one example, there are a lot of examples like this where slopes play a very important role. So, what is the slope?
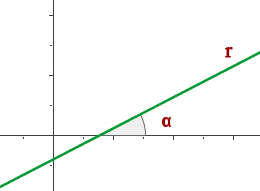
The slope or gradient is the inclination of a line with respect to the x-axis. Basically, the slope is the ratio of the amount of increment in y per unit of x. In short, it shows how steep your line is. For linear geometry, the slope remains the same throughout the graph. However, for curves, the slope changes at every point. Finding the slope of a curve is a big discussion, therefore, let's stick with the line for now. Usually, the slope is denoted by the letter m.
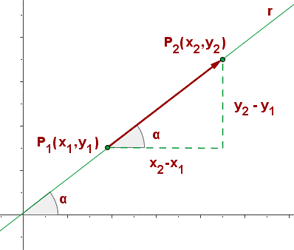
Consider the above graph. You have two points,  and
and  . Furthermore, you are also provided with angles and all you need to do is to find the slope of the line. There are a few methods through which you can find the slope.
. Furthermore, you are also provided with angles and all you need to do is to find the slope of the line. There are a few methods through which you can find the slope.
Finding slope using two points
To find the slope by using the coordinates, you need to have two different points of the same line. For the above example, you have  and
and  . Using those coordinates, we can find the slope like this:
. Using those coordinates, we can find the slope like this:
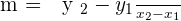
Just place the values of xs and ys and find the slope.
Finding slope using the angle
We usually use the cartesian coordinate system but in the case of the polar coordinate system, there are some changes. In the polar coordinate system, our y values are in terms of  and x values are in
and x values are in  . Since slope is the ratio of increment in y per unit x, therefore, in the polar coordinate system, it would be like this:
. Since slope is the ratio of increment in y per unit x, therefore, in the polar coordinate system, it would be like this:
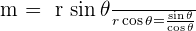
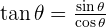
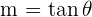
All you need to do is input the value of  or
or  and use the
and use the 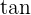 trigonometric ratio to find the slope of the line.
trigonometric ratio to find the slope of the line.
Finding slope using the vector of the line
Working with vectors is tricky. The gradient is in the form of 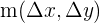 in vectors. The delta means a resultant in the value, therefore, the deltas you see in both variables means that the values of x and y are obtained by subtracting from the initial value. Suppose,
in vectors. The delta means a resultant in the value, therefore, the deltas you see in both variables means that the values of x and y are obtained by subtracting from the initial value. Suppose,  , that means,
, that means, 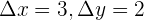 . We all know that vectors have two values, the starting point, also known as the tail of a vector
. We all know that vectors have two values, the starting point, also known as the tail of a vector 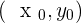 , and the ending point, also known as the head of a vector
, and the ending point, also known as the head of a vector 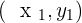 . The resultant values mean that the coordinates' ending points were subtracted from the initial point (i.e.
. The resultant values mean that the coordinates' ending points were subtracted from the initial point (i.e.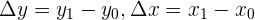 ). Once you obtained the values of
). Once you obtained the values of  &
&  , just use the below formula to calculate the slope:
, just use the below formula to calculate the slope:

Finding slope using the equation of the line
There are two methods to find the slope of the line using the equation of the line. The first one is lengthy but it is the right way to find the slope and the second one is the shortcut. Here is the lengthy method, usually you will see equations of a line like this, 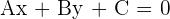 . The
. The 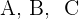 are the coefficients, and
are the coefficients, and  are the coordinates. You need to transform the
are the coordinates. You need to transform the 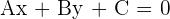 into
into  . Below is how you should transform the
. Below is how you should transform the 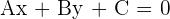 into
into  :
:
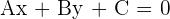
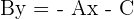

Compare the above equation with 



Still wondering what is the shortcut? Take a look at the last step,  . Just input the value of A and B in their places and don't forget about the minus sign and there you go! You just found the slope of a line using the equation.
. Just input the value of A and B in their places and don't forget about the minus sign and there you go! You just found the slope of a line using the equation.
Important Points to Note
There are some things that you need to note to save your time and effort.
- If two lines are parallel then their slopes are equal,
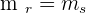 .
. - If two lines are perpendicular to each other then their slopes are the inverse of each other and their signs are opposite,
 .
. - If the is vertical, i.e. all values of x are constant, then the slope will be infinity,
 . However, if the line is horizontal, i.e. all values of y are constant, then the slope will be zero.
. However, if the line is horizontal, i.e. all values of y are constant, then the slope will be zero. - If the angle between the line with the positive x-axis is acute, the slope is positive and grows as the angle increases. However, if the angle between the line with the positive x-axis is obtuse, the slope is negative and decreases as the angle increases.