Imagine that there is a hill in front of you. The hill is a little steep but you can climb it. Imagine the same hill but more steeper than the last hill. Now climbing that hill will be a lot difficult. That steepness is called gradient in mathematical language. Basically, a gradient is the rate of change of ordinate by the rate of change of abscissa. In some textbooks, you will also learn that gradient is the change in height by the change in horizontal length (or in short words, rise by run). They all mean the same but how do we find gradient? What is the importance of gradient in the world of mathematics? Let's find out!

How to Find Gradient
Since the gradient is the rate of change of ordinate by the rate of change of abscissa, let's convert this into mathematical language.
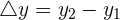
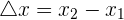
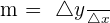
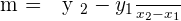
where m is the gradient.
In the above formula, you need 2 coordinates of the x-axis as well as the y-axis. What if you are not given any coordinates and still asked to find the gradient? That is why there are a few more formulas that will find the gradient of any line. Let's say you are given an angle from normal and asked to find the gradient then you should use this formula:

All you need to do is to insert the angle in 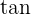 and you can get the gradient. What if you are given only the equation of the line and asked to find the gradient? For example, find the gradient of this line
and you can get the gradient. What if you are given only the equation of the line and asked to find the gradient? For example, find the gradient of this line 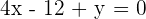 . There are two methods of finding the gradient. The first is simple but it requires effort. You need to make the equation in terms of y and then compare it with
. There are two methods of finding the gradient. The first is simple but it requires effort. You need to make the equation in terms of y and then compare it with  .
.
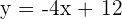

Comparing the above equations:

Where m is the gradient and c is the y-intercept.
Hence, we got our gradient which is  . However, this method limitation is that you can apply it to a linear equation only. If you are given any other equation, except linear, you can't use this method.
. However, this method limitation is that you can apply it to a linear equation only. If you are given any other equation, except linear, you can't use this method.
The second method requires knowledge of differentiation. If you know how to find differentiation then you can easily find the gradient. The advantage of this method is that you can apply to any equation. The differentiation of any equation will give you the value of the gradient. Here is how you can find the gradient of any equation:
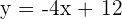
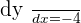
Hence the gradient is -4. Here is another example but on a quadratic equation.
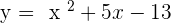 , find the gradient on the point when
, find the gradient on the point when  .
.
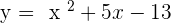
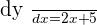
When  :
:
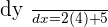
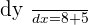
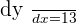
Hence on  , the gradient is
, the gradient is  .
.
Examples
Calculate the point-slope form equation of the line passing through points A = (−2, −3) and B = (4, 2).
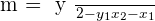
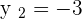
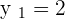
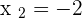
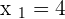
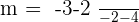
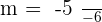
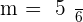

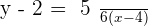
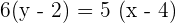
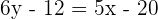
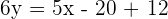
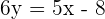
Calculate the equation of the line with a slope of 45° which passes through the point (−2, −3).

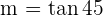
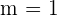

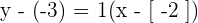
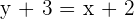
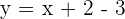

Find the gradient of this equation 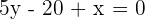 .
.
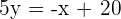
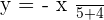
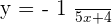

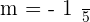
Find the gradient of this equation 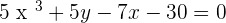 at point when
at point when 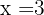 .
.
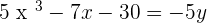
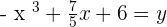
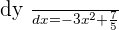
When  :
:
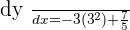
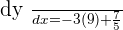
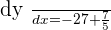
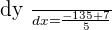
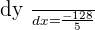
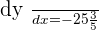
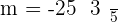
Gradient Applications
Finding slope isn't just a part of mathematics, it contributes to many other things. One of the biggest contributions is in Newtonia physics. Newton's second law states that the force is the product of mass and acceleration in the direction of acceleration. At this point, you might be wondering what is the relation of Newton's law with slope? If you noticed, the formula of acceleration is the same as the formula of the slope. This means that the slope of a line or curve of a velocity-time graph is the acceleration. It means that you are basically multiplying mass with the slope to find the force.
In addition, the concept of the gradient is used widely in many engineering practices. Basically, gradient means the rate of change. Applications such as heat transfers, mass transfer, momentum transfer, and a few more are based on different gradients. For example, heat transfer occurs because of the temperature gradient, momentum transfer occurs because of the velocity gradient.
In addition, concept of the gradient is also widely used in differentiation and integration. For example, if you derivate the gradient (that means you derivate the same equation twice), you can find the maximum or minimum points.
Summarise with AI:













