Chapters
The graph of a linear equation in an x-y plane is a straight line. Linear equations can be written in different forms. One of the forms of linear equations is two-point form also known as point slope form. In this article, we will focus on two-point form of the linear equation.
We will discuss the following topics related to two-point form of the linear equations in detail along with the relevant examples:
- Writing an equation of a straight line in two-point form
- Converting two point-form into the slope intercept form of the linear equation
- Converting two-point form into the standard form of the linear equation
Besides writing the equations into a two-point form from the given set of values and graphs, we will also see how to write the linear equations in two-point form from the given scenarios.

Write an equation of a straight line in two-point form
Two-point form formula
 and
and in two-point form is given below:
in two-point form is given below: 
In the above formula, the slope is denoted by m.
Slope formula
To write the equation of a straight line in a two-point form, first find the slope denoted by “m” of the straight line. The formula for the slope of the straight line is given below:
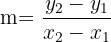
Some Facts about Slope
Some interesting useful facts about slope are given below:
- The slope can be zero or non-zero (positive or negative).
- Zero slope means that no matter what the value of the x-coordinate is, the y-coordinate remains constant. The graph of an equation will be a horizontal line, if slope is zero.
- A positive slope means that there is positive relationship between x and y variables. It means that as the value of x- coordinate increases, the value of y also increases or if the value of x decreases, then the value of y also decreases.
- A negative slope means that the two variables are negatively related to each other. It means that as the value of x increases, the value of y decreases or if the value of x decreases, the value of y increases.
- The slope of two parallel lines is same, whereas the slope of two perpendicular lines are negative reciprocals of each other.
Example 1
Write the equation of the line passing through the points 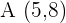 and
and  .
.
Solution
To write the equation, first find the slope of the equation. From the above two points we get the following values of  and
and  intercepts.
intercepts.
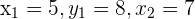 and
and 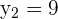
Substitute these values in the following formula:
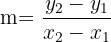
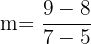
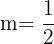
Now, put the values of 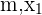 and
and 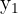 in the formula
in the formula  to get the equation in two point form passing through the points
to get the equation in two point form passing through the points  and
and 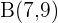 :
:
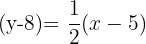
Example 2
Now, we will see how can we write an equation of a straight line in point-slope form given the graph of an equation in a coordinate plane. Consider the following graph:

Solution
Take two points from the graph. Suppose we take  and
and  . In the above graph,
. In the above graph, 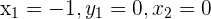 and
and 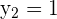 . To write the equation in two-point form, first we need to find the slope by substituting these values in the formula below:
. To write the equation in two-point form, first we need to find the slope by substituting these values in the formula below:
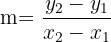
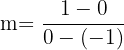
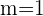
Now, put the values of the  ,
,  and
and 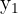 in the following formula to get the equation in two-point form:
in the following formula to get the equation in two-point form:

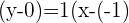
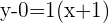
Example 3
It is not always necessary that two points on the line are given in a question. Sometimes, the slope,  and
and  intercepts of one point are given. Consider the example below:
intercepts of one point are given. Consider the example below:
Write the equation of a straight line in two-point form having a slope of  passing through the points
passing through the points 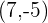 .
.
Solution
In the above example, 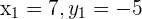 , and
, and  .
.
Put these values in the two-point form of the equation:
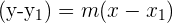
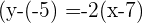
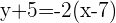
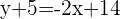
Example 4
You can also write the equation in a two-point form from the given scenario. Consider the following situation:
James joined the fitness club to lose an average weight of 7 pounds each month. At the end of the sixth month, his weight was 148 pounds. Write the given scenario in two point form.
Solution
Since he lost 7 pounds each month, hence the slope  is
is  .
.
It is given that at the end of the sixth month, his weight was 148 pounds. We will take months as an independent variable and weight as a dependent variable.
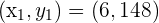
Solve the equation by substituting the values of  , and
, and 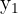 in the following formula to get the point slope form of the linear equation.
in the following formula to get the point slope form of the linear equation.

Converting two-point form into slope-intercept form of the linear equation
Now, we know how to write an equation of the line in a two-point form also known as point-slope form. Do you know that besides a two-point form linear equation can also be written in two other forms? These forms are standard and slope-intercept form.
In this section, we will discuss how to convert the two-point form into the slope-intercept form of the linear equation. If you are given two points on the line, you can write the equation in slope-intercept form. But to do so, you first need to write the equation in a two-point form. The formula for a slope-intercept form is given below:

Here, m is the slope and b is y-intercept of the line.
Let’s see how to convert the equation from point-slope form to slope-intercept form from the following examples.
Example 1
Write the equation of the line in slope-intercept form passing through the points  and
and 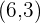 .
.
Solution
In the above example, 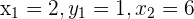 and
and 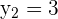 .
.
First find the slope using the formula below:
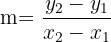
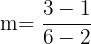
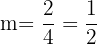
Now, write the equation of a line in point-slope form of the linear equation:

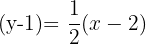
We will get the following form by simplifying the right hand side of the equation:
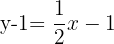
Isolate  on the left side by adding 1 to both sides of the equation:
on the left side by adding 1 to both sides of the equation:
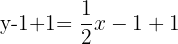
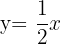
Hence, the slope-intercept form of the line passing through the points  and
and 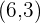 is
is 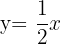 . [Note that the slope-intercept form of the straight line is
. [Note that the slope-intercept form of the straight line is  . If the equation of the line takes the form of
. If the equation of the line takes the form of  , then it means that the value of b which is the y-intercept of the line is 0.].
, then it means that the value of b which is the y-intercept of the line is 0.].
Example 2
Write the equation in slope-intercept form passing through the points  and
and 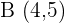 .
.
Solution
First find the slope of the line using the following formula:
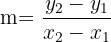
In the above example,  , and
, and 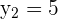 .
.
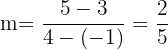
Now, put the values of 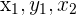 , and
, and 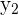 into the point-slope form of the equation:
into the point-slope form of the equation:
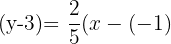
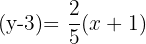
The slope will be multiplied by the term inside the brackets to get the point-slope form:
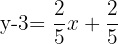 (Point slope form)
(Point slope form)
To convert this equation from point-slope form to slope-intercept form, solve the first equation by taking -3 on the right hand side of the equation.
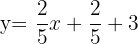
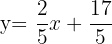 (Slope intercept form)
(Slope intercept form)
Example 3
We can also write the equation in a two-point form or slope-intercept form from the scenario. Sometimes the situation demands writing linear equations in the two-point form first before converting them into the slope intercept form. The example of one such scenario is given below:
Sarah got a new job and decided to save a fixed part of her salary each month. She already had some savings from her previous job. After starting a new job, she had 2110 dollars of savings in two months and in five months her total savings amounted to 3400 dollars.
- How much salary did she save each month?
- Write an equation that can be used to determine her salary in
 number of months.
number of months. - How much savings she already had before she started the new job?
Solution
We can write the information in the form of a table. In two months, her savings were 2110 dollars and in five months her total savings amounted to 3400 dollars.
| Months (x) | Savings (y) |
|---|---|
| 2 | 2110 |
| 5 | 3400 |
Part 1
To find the fixed amount she saved each month, first find the slope of the linear equation from the above table:
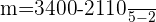
=
=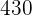
Hence, she saved 430 dollars each month.
Part 2
To write an equation that can be used to determine her savings after  number of months, we need to find the slope-intercept form of the equation. But before finding the slope-intercept form, first, we need to write the equation in a two-point form.
number of months, we need to find the slope-intercept form of the equation. But before finding the slope-intercept form, first, we need to write the equation in a two-point form.

 (Point slope form)
(Point slope form)
Convert the above equation into slope-intercept form by simplifying the right side of the equation.

Isolate  on the left hand side by adding 2110 on both sides of the equation:
on the left hand side by adding 2110 on both sides of the equation:
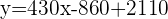
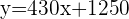 (Slope-intercept form)
(Slope-intercept form)
Hence, you can use your calculators to determine her savings after  number of months from the equation
number of months from the equation 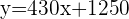 .
.
Part 3
In the previous part, we determined the Slope intercept form of the equation from the scenario. In the equation, 1250 represents the  -intercept of the equation. The point at which the line intersects the
-intercept of the equation. The point at which the line intersects the  axis is known as
axis is known as  -intercept of the line. At this point of intersection the value of
-intercept of the line. At this point of intersection the value of  intercept is 0.
intercept is 0.
To find the savings she already had before starting the new job, put  in the equation
in the equation 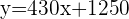 .
.
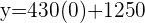
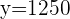
Hence, the correct answer is 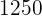 dollars.
dollars.
Converting two-point form into the standard form of the linear equation
The standard form of a linear equation is given by the following formula:

Example 1
We can easily convert the two-point form of the linear equation into a standard form. Consider the following equation in the two-point form:

Solution
To convert it into the standard form, the slope of a line which is 2 will be multiplied by the term 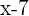 on the right hand side of the equation:
on the right hand side of the equation:

Isolate y on the right hand side of the equation by adding 3 on both sides:
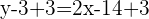

We will add 11 on both sides of the equation to get the following equation:
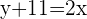
We know that the standard form of the equation is  , therefore we will isolate the constant by subtracting
, therefore we will isolate the constant by subtracting  on both the sides:
on both the sides:

Here, 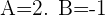 and
and  .
.
Example 2
Consider the second example below:
Write the equation of the line in the standard form passing through the points  and
and 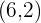 .
.
Solution
To write the equation in standard form, first find the equation in two-point form. We will begin it by finding the slope of the equation.
In the above example,  and
and 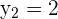 .
.
By putting these values in the slope formula, we will get the following value of slope:
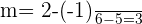
Now, we know the value of the slope, we can easily get the two-point form by plugging it in the following formula:
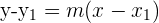
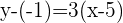
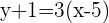 (Two-point form)
(Two-point form)
By multiplying the slope with the term inside the brackets, we will get the following equation:
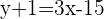
Isolate y on the left hand side by subtracting 1 from both sides of the equation.
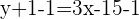
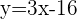 (Slope intercept form)
(Slope intercept form)
The standard form of the equation is  . Hence take -16 to the left hand side and y to the right hand side of the equation to get the final equation.
. Hence take -16 to the left hand side and y to the right hand side of the equation to get the final equation.
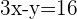 (Standard form)
(Standard form)
Here, 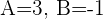 , and
, and 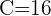 .
.
Summarise with AI:













