Chapters
In many cases, lines and curves touch ordinate and abscissa. Now you might be wondering why they are important? When a line or curve touches an axis, all the coordinates, except the coordinate of the line touches, become zero. It helps us to find the value of the coordinate. Finding x- and y-intercepts are easy, however, to understand this concept, you should know about graphical equations. If you don't know about graphical equations, we strongly recommend you go through them first to understand x- and y-intercepts.
There are two types of intercepts, one is the x-intercept and the other is the y-intercept. Let's say you have an equation, 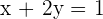 . Since this line doesn't have a limit, we can say it will surely pass through the x-axis as well as the y-axis. When it passes from the x-axis, one thing is for sure, the value of y will be equal to zero. This is because, at any coordinate of x on the x-axis, the coordinate of y will always be equal to zero. Hence, the coordinates we will get will be in form of this,
. Since this line doesn't have a limit, we can say it will surely pass through the x-axis as well as the y-axis. When it passes from the x-axis, one thing is for sure, the value of y will be equal to zero. This is because, at any coordinate of x on the x-axis, the coordinate of y will always be equal to zero. Hence, the coordinates we will get will be in form of this, 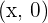 , we call it x-intercept. On the other hand, the same method is applied for the y-intercept but the only change will be that at any coordinate of y, the value of x will be equal to zero. We will call it the y-intercept.
, we call it x-intercept. On the other hand, the same method is applied for the y-intercept but the only change will be that at any coordinate of y, the value of x will be equal to zero. We will call it the y-intercept.

x-Intercept
Let's try to understand this concept with the help of an example. We have an equation,  . To find the value of the x-intercept, we need to replace the y with zero.
. To find the value of the x-intercept, we need to replace the y with zero.




y-intercept
Let's pick up the same example and try to find the y-intercept. To find the y-intercept, you need to replace all x variables with zero.
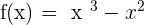

Hence, the y-intercept is also zero, but did you note something? One of the answers of the x-intercept is the same as the y-intercept (i.e.  ). Does it mean that the answer of y-intercept can be equal to the answer of x-intercept? Yes but only in the case of origin. If one of the intercepts is at the origin, it means both intercepts are there. However, this possibility is rare. Let's take another example where the y-intercept is not equal to zero.
). Does it mean that the answer of y-intercept can be equal to the answer of x-intercept? Yes but only in the case of origin. If one of the intercepts is at the origin, it means both intercepts are there. However, this possibility is rare. Let's take another example where the y-intercept is not equal to zero.
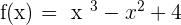

Hence, the y-intercept of the above example is 
Exercise
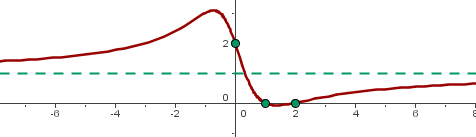
For the following function, find the intersections with the x- and y-axis:
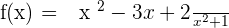
x-intercepts
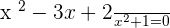
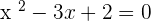
After solving the equation, our x-intercepts will be:

y-intercept
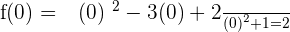
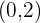
Summarise with AI:












I have math qstn problm
Break even point