Chapters

What are Fractions?
There are two numbers in the fractions, a numerator, and a denominator. The number at the top is known as a numerator and it represents the number of parts/pieces you have. The number below is known as the denominator and it represents the total number of parts/pieces.
For example, a fraction  represents three parts of a quarter. We can have a numerator greater than or smaller than the denominator. For instance,
represents three parts of a quarter. We can have a numerator greater than or smaller than the denominator. For instance,  means 9 parts, where each part is a quarter of a whole.
means 9 parts, where each part is a quarter of a whole.
While dealing with fractions, you should keep the following points in mind:
- If the numerator and denominator of a fraction are equal, then it is equal to 1. For example, the fractions
 ,
,  and
and 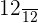 are equal to 1 because their numerators and denominators are equal.
are equal to 1 because their numerators and denominators are equal.
- If the numerator of the fraction is 0, then the whole fraction is equal to 0. For example,
 is equal to zero because the numerator is zero.
is equal to zero because the numerator is zero.
- The denominator of the fraction cannot be zero.
- When we write a whole number, then we assume that its denominator is equal to 1. For example, the denominators of the numbers 3, 8, 9, 2, 6, and 10 are equal to 1. In other words, we can say that a fraction that has 1 in its denominator is equal to its numerator.
Types of Fractions
There are three types of fractions.
1. Proper Fractions
The fraction in which the numerator is less than the denominator is known as a proper fraction. For example, 
 and
and 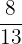 are proper fractions because the numerators of these fractions are less than their denominators.
are proper fractions because the numerators of these fractions are less than their denominators.
2. Improper Fractions
The fraction in which the numerator is greater than the denominator is known as an improper fraction. For example, 
 and
and  are improper fractions because their numerators are greater than their denominators.
are improper fractions because their numerators are greater than their denominators.
3. Mixed Fractions
These fractions are written by combining a whole number and a fraction. For example, 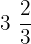 ,
,  and
and 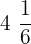 are mixed fractions because they are comprised of whole numbers and fractions.
are mixed fractions because they are comprised of whole numbers and fractions.
Converting Improper Fractions to Mixed Fractions
Do you know that we can convert improper fractions to mixed fractions and vice versa? You may be wondering how to do that. It is very simple. You just divide the numerator by the denominator and write quotient as a whole number part of the mixed fraction and remainder in the numerator. Consider the following example:
Convert  into a mixed fraction.
into a mixed fraction.
When we divide 9 by 4, we will get 2 as a quotient and 1 as a remainder. Hence, we can write it as a mixed fraction in this way:
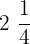
Converting Mixed Fractions to Improper Fractions
We can also convert mixed fractions to improper fractions by multiplying the denominator with the whole number part of the fraction and adding the numerator to it. The resulting number we get after applying these series of multiplication and addition operations is written in the numerator and the denominator remains as it is. Consider the following example:
Convert 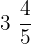 into an improper fraction.
into an improper fraction.
First, we will multiply the denominator 5 with the whole number 3 to get 15. Then, we will add 4 to it to get 19. We will write the number 19 as a numerator and the denominator will remain as it is. Hence, the final fraction is 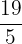 .
.
Dividing Fractions
Like numbers, we can apply the arithmetic operations of addition, subtraction, multiplication, and division on fractions. In this section, we will see how to divide fractions.
How to Divide Fractions?
To divide fractions, we take the reciprocal of the second fraction and solve the resulting fractions through multiplication. In other words, after taking the reciprocal, we remove the division sign and replace it with multiplication. Taking reciprocal means inverting the fraction in such a way that the numerator becomes the denominator, and the denominator becomes the numerator.
In the next section, we will solve some examples which will make the whole concept clear.
Example 1
Solve  :
: 
Solution
The ratio symbol ":" means we have to divide the fractions. We will take the reciprocal of the second fraction and substitute the division sign with the multiplication one:
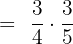
Multiplying fractions is straightforward as we just multiply the numerator with the numerator and denominator with the denominator.
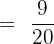
Example 2
Solve  :
:  .
.
Solution
We will take the reciprocal of the second fraction and substitute the division sign with the multiplication one:
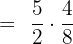
By multiplying the numerators and denominators together, we will get the following fraction:
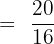
To simplify the above fraction, we will divide the numerator and denominator by 4 because they are multiples of 4. Hence, the simplified form of the fraction is:

Example 3
Solve  :
:  .
.
Solution
We will take the reciprocal of the second fraction and substitute the division sign with the multiplication one like this:
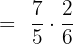
By multiplying the numerators and denominators together, we will get the following fraction:
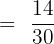
Since, both the numerator and the denominator are multiples of 2, therefore we can simplify the above fraction further.
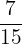
Example 4
Solve 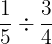
Solution
We will take the reciprocal of the second fraction and substitute the division sign with the multiplication one like this:
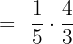
By multiplying the numerators and denominators together, we will get the following fraction:
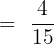
The above fraction cannot be simplified further.
Example 5
Solve  :
:  and convert the answer into a mixed fraction.
and convert the answer into a mixed fraction.
Solution
We will take the reciprocal of the second fraction and substitute the division sign with the multiplication one:
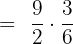
By multiplying the numerators and denominators together, we will get the following fraction:
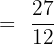
Note that the above fraction can be simplified further because both the numerator and the denominator are multiples of 3. Hence, the simplified form of the fraction is:

We have got an improper fraction by dividing the two fractions. To convert it into the mixed fraction, we will divide the numerator by the denominator. By doing so, we will get the quotient 2 and remainder 1. Using these values, the mixed fraction will be:
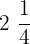
Example 6
Sarah is baking cookies and she had  of the total ingredients left. Each cookie consumes
of the total ingredients left. Each cookie consumes 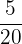 of the total ingredients. How many cookies can Sarah bake with the remaining ingredients?
of the total ingredients. How many cookies can Sarah bake with the remaining ingredients?
Solution
Ingredients left = 
Ingredients required to bake a single cookie = 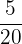
Number of cookies that can be baked = Ingredients left : Ingredients required to bake a single cookie
=  :
: 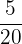
=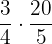
= 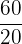
After simplifying the above fraction, we will get the following number of cookies:
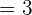
Sarah can bake 3 more cookies from the remaining ingredients.
Example 7
Alice has 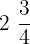 of the total pizza left. She cuts the slices that are
of the total pizza left. She cuts the slices that are  of the whole pizza. How many slices of pizza does she have?
of the whole pizza. How many slices of pizza does she have?
Solution
Pizza left = 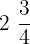
Since the above fraction is in the mixed form, hence we need to convert it into an improper form to solve this example.
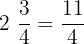
The size of each slice = 
Number of slices = Pizza left : Size of each slice
= 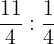
= 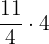
= 
Hence, Alice cut the pizza into 11 slices.













