Converting Exact Decimals to Fractions
Exact or Non-Repeating Decimals
An exact decimal number is a decimal number that terminates, meaning it has a finite or exact amount of numbers to the right of the decimal point.
Examples
All of these are examples of exact decimals. Even though the last example did repeat once, it didn't repeat infinitely many times.
An exact decimal does not have any infinitely repeating patterns, such as
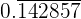
where the line over the numbers represents an infinitely repeating pattern of those numbers.
Conversion
When we want to convert an exact decimal into a fraction 
, we must first form a fraction out of that decimal number.
We do this by making the decimal number itself the numerator 
and placing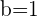 
in the denominator.
Example
Let's choose as our decimal number. Then
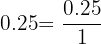
We get rid of the decimal point in the numerator by moving it to the right the number of places to where it is not needed anymore.
For , we would move the decimal point to the right two spaces, to the right of the 
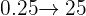
Next, we add the same exact number of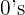 
to the right of the 
in the denominator as the number of places we moved the decimal point in the numerator.
So we add two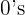 
to the right of the
This process forms an equivalent fraction to our original fraction that does not have the decimal point in the numerator
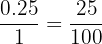
After we form the correct fraction to represent the initial decimal, we need to simplify it if possible
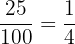
It helps to remember this rule:
We add the number of 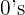to the right of the in the denominator that equals the number of places we moved the decimal point to the right to get rid of it.
Example
Convert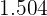 
into a fraction.
First, we divide 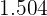by to form a fraction
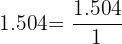
Then move the decimal point right three places and add three 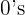to the right of the
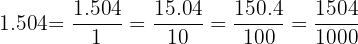
Here we showed all of the intermediate steps that show the processes of moving the decimal point to the right and adding the same amount of 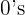simultaneously.
Next, simplify
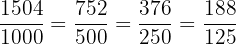
Example
Convert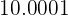 
to a fraction
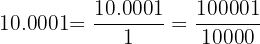
Converting a Repeating Decimal to Fraction
What if we have a decimal that repeats? How do we find the answer to a problem like that?
Example
Say we have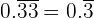 
. You may know that this repeating decimal's fractional value is just 
, but how do we actually get to this answer?
There is a Mathematical trick that we can employ where we just divide the numbers to the right of the decimal by the same amount of 
placed next to each other, like 
, 
, 
...
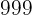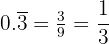
We have one 
repeating to the right of the decimal, so we divided it by one .
Example
Convert 
to a decimal
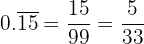
We have two numbers 
in a repeating pattern, so we divided by two 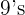to make
If there are one or more numbers to the left of the decimal, we still divide by the same amount of 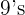as there are to the right of the decimal, but we will need to subtract the number that appears to the left of the decimal from the number that is formed by combining the numbers to the right and to the left of the decimal point.
Example
Convert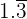 
to a decimal
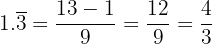
The numerator was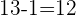 
because 
was the number formed by combining all of the numbers and was the number to the left of the decimal point, so we had to subtract it from , which results in 
. Then we divided by one because one number was repeating.
Here is the rule for a decimal that repeats after an initial amount of non-repeating decimals
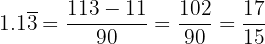
We subtract 
from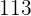 
because that is the total number of digits that don't repeat.
We divide by one because of the repeating pattern of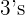 
and add a 
to the right for the one non-repeating number to the right of the decimal point .
Find more Maths teacher here on Superprof.
Did you like this article? Rate it!
Loading...
