Chapters
Addition of Fractions with Same Denominators
Adding two fractions that have the same denominator is straightforward. We just add the numerators of each fraction together and keep the same denominator.
Example
Add 
to 
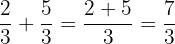
Addition of Fractions with Unlike Denominators
Say we want to add 
to 
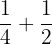
We can’t just add the numerators and denominators to find the answer, because the denominators of both fractions are not equal.
The trick is to find a common (same) denominator for both fractions that will allow us to properly add them.
What number can we choose that both 
and 
will divide into evenly?
Our best choice would be because we always want to choose the smallest such number.
We could choose any number we want that is divisible by both and , such as 
, and it will work. It just saves us time if we choose the smallest one, as we will see shortly.
already has a in the denominator, so our job is to make into an equivalent fraction that has a in the denominator.
The equivalent fraction to with a in the denominator is 
.
Now, we are in a position to add them together
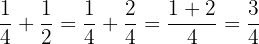
Common Denominators and Multiplication by 1=a/a
The addition of 2 fractions involves the processes of finding a common denominator, preferably the Least Common Denominator, of both fractions and equivalent fraction conversion in order for us to properly add them.
Finding the common denominator in the last example was relatively easy because is a multiple of .
Here we will outline the actual technique for finding a common denominator.
Example
Add and 
To perform this problem we must multiply each fraction by an equivalent form of the number 
that will make each fraction have a common denominator.
What is the first number that both denominators 
and divide into evenly?
In this case, it is just 
How do we make each fraction into an equivalent form that has a denominator of 
?
We multiply each fraction by so to speak
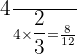
and
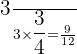
Notice that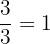 
and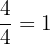 
.
Now we've put ourselves in a position to add these fractions
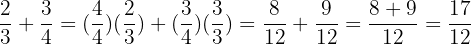
We multiplied both fractions by a form of in order to find a common denominator: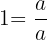 
for the first and 
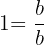for the second.
Example
Add
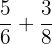
Find the first number that both 
and 
divide into evenly: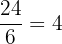 
and 
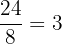
Multiply each fraction by an equivalent form of that makes its denominator 
: 
for 
and 
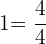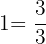for 
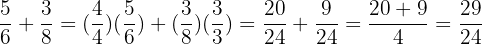
Example
Add
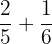
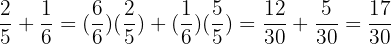
Addition of 3 or more Fractions
The addition of 3 or more fractions is performed the same way but we now have 3 or more denominators to account for in finding a common denominator.
Example
Add
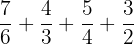
Find a common denominator for 
and . It is .
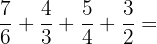
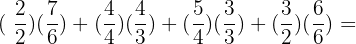
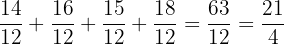
Quick and Easy Formula
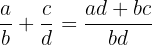
Find more Maths tutors near me here on Superprof.
Did you like this article? Rate it!
Loading...
