Chapters

The best Maths tutors available
Exercise 1
Calculate:
1 
2 
3 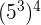
4 
5 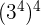
6 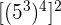
7 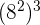
8 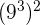
9 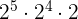
10 
11 
12 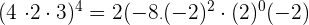
13 
14 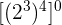
15 
16 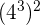
Exercise 2
Calculate:
1. 
2 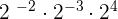
3 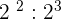
4 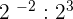
5 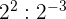
6 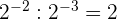
7 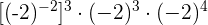
8 
Exercise 3
Calculate:
1 
2 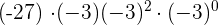
3 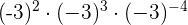
4 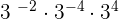
5 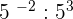
6 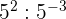
7 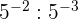
8 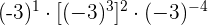
Exercise 4
Calculate:
1 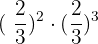
2 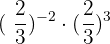
3 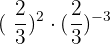
4 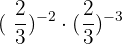
5 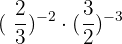
6 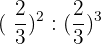
7 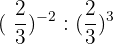
8 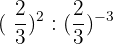
9 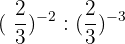
10 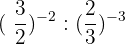
11 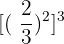
12 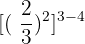
13 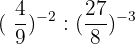
Exercise 5
Calculate:
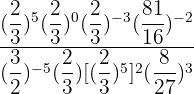
Exercise 6
Calculate:
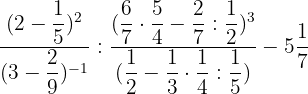
Exercise 7
Calculate:
1 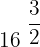
2 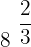
3 
4 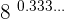
Solution of exercise 1
Calculate:
1 
2 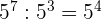
3 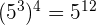
4 
5 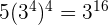
6 
7 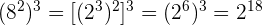
8 
9 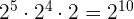
10 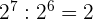
11 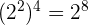
12 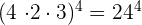
13 
14 
15 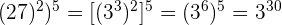
16 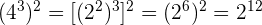
Solution of exercise 2
1. 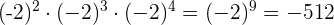
2 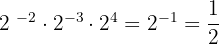
3 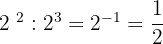
4 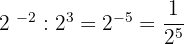
5 
6 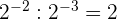
7 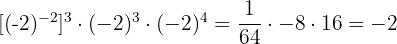
8 
Solution of exercise 3
1 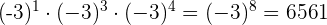
2 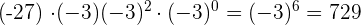
3 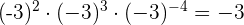
4 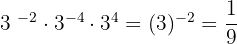
5 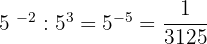
6 
7 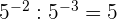
8 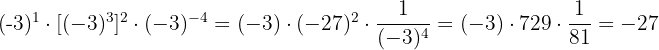
Solution of exercise 4
Calculate:
1 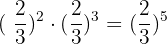
2. 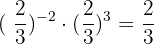
3 3 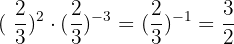
4 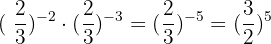
5 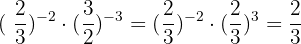
6 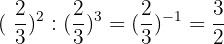
7 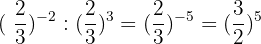
8 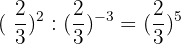
9 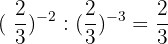
10 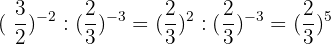
11 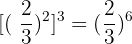
12 12 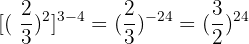
13 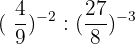
 [(\frac{2}{3})^2]^{-2} : [ (\frac{3}{2})^3]^{-3} = (\frac{2}{3})^{-4} : (\frac{3}{2})^ {-9}
[(\frac{2}{3})^2]^{-2} : [ (\frac{3}{2})^3]^{-3} = (\frac{2}{3})^{-4} : (\frac{3}{2})^ {-9} =
= 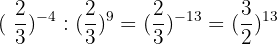
Solution of exercise 5
Calculate:
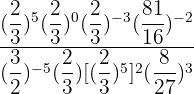
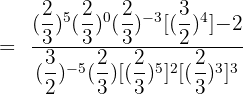
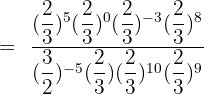
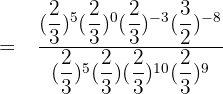
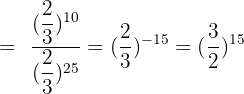
Solution of exercise 6
Calculate:
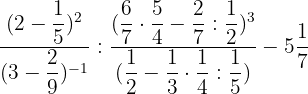
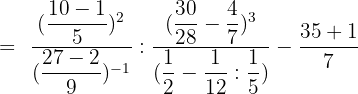
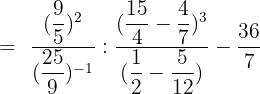
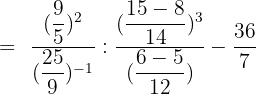
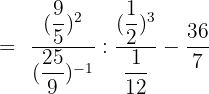
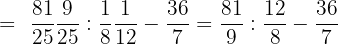
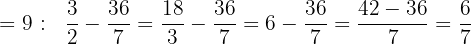
Solution of exercise 7
Calculate:
1 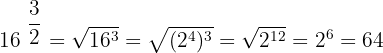
2 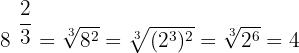
3 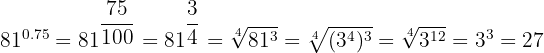
4 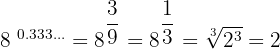
Summarise with AI:













