Chapters

Introduction to Fractions
A fraction is comprised of two numbers, a numerator which is the number at the top, and a denominator that is below the numerator. Generally, a numerator shows the number of elements/parts that a person has. On the other hand, a denominator shows the total number of elements/parts.
For example, consider the following scenario.
There are 18 chocolates in a packet. Your share is two-sixths of all the chocolates and your younger brother's share is four-sixths of all the chocolates. How will you represent this information numerically?
Well, your share can be represented in the form of a fraction as two divided by six. Mathematically, it will be written as:

Your younger brother's share will be represented as four divided by six. We will represent it mathematically as:

In a fraction, a numerator can be either greater than or smaller than the denominator. Based on the values of the numerator, denominator, and how we write fractions, we classify them into the following three broad categories:
- Proper Fractions: In these fractions, the numerator is always smaller than the denominator. For example,
 ,
, 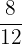 , and
, and 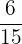 are proper fractions because the numerators are less than the denominators.
are proper fractions because the numerators are less than the denominators.
- Improper Fractions: In these types of fractions, the numerator is always greater than the denominators. For example,
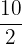 ,
,  , and
, and  are improper fractions because the numerators are greater than the denominators.
are improper fractions because the numerators are greater than the denominators.
- Mixed Fractions: These fractions combine the whole number and a fraction. For example,
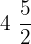 .
. 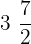 and
and 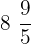 are mixed fractions as they are written by combining the whole numbers and fractions.
are mixed fractions as they are written by combining the whole numbers and fractions.
Converting Fractions From One Form to Another
Do you know that we can convert improper fractions to mixed fractions and mixed fractions to improper fractions? In this section, we will discuss how to do that.
Improper Fraction to a Mixed Fraction
Converting an improper fraction to a mixed fraction is straightforward. To do so, you just need to be aware of a simple division process. Divide the numerator by the denominator and write the quotient as a whole number and remainder in the numerator. The denominator will remain as it is. Consider the following example.
Convert 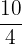 into a mixed fraction.
into a mixed fraction.
When we will divide 10 by 4, we will get the quotient 2 and remainder 2. We will write it as a mixed fraction using this information like this:
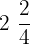
Mixed Fraction to an Improper Fraction
A mixed fraction can also be converted into an improper fraction. To do so, we simply multiply the denominator with the whole number and add a numerator to it. The resulting number we obtain is written as the numerator and the denominator remains the same in the new fraction. Consider the following example.
Convert 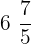 into an improper fraction.
into an improper fraction.
First, we will multiply the denominator that is 5 in the above example with the whole number 6. After multiplying, we got the number 30. Now, we will add the numerator that is 7 in this number to get the numerator of the new fraction. 30 + 7 is equal to 37. The denominator will remain as it is. Hence, the new fraction will be:
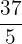
Multiplying Fractions
We can apply the arithmetic operations of addition, subtraction, multiplication, and division on fractions just like numbers. In this section, we will specifically discuss how to multiply two fractions together. We multiply two fractions by multiplying the numerator with numerator and denominator with denominator. Let us understand this concept further through the following examples.
Example 1
Solve 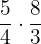 and tell the type of the new fraction.
and tell the type of the new fraction.
Solution
The numerator will be multiplied by the numerator and denominator with the denominator like this:
=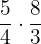
=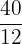
To simplify the above fraction, we will divide the numerator and denominator by 4.
=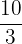
The above fraction is in the improper form because the numerator is greater than the denominator.
Example 2
Solve 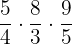 .
.
Solution
The numerator will be multiplied with the numerator and the denominator will be multiplied with the denominator.
=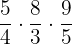
=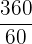
The fraction can be simplified further because 360 is a multiple of 60.
Example 3
Solve 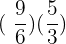 and write the answer as mixed fraction.
and write the answer as mixed fraction.
Solution
Multiply the numerators and denominators together to get a new fraction like this:
=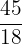
The above fraction is in improper form and we have to write the answer as a mixed fraction. We can easily convert the fraction 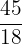 into a mixed fraction by following a simple division process. The highest number that is a multiple of 18 but less than 45 is 36. 18 into 2 is equal to 36, hence the quotient is 2. The remainder is 9 which is obtained by subtracting 45 from 36. The answer in mixed fraction form will be written like this:
into a mixed fraction by following a simple division process. The highest number that is a multiple of 18 but less than 45 is 36. 18 into 2 is equal to 36, hence the quotient is 2. The remainder is 9 which is obtained by subtracting 45 from 36. The answer in mixed fraction form will be written like this:
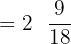
Example 4
Solve 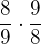 .
.
Solution
Both the fractions are multiplicative inverses of each other. A multiplicative inverse of a fraction is it's reciprocal. While working with fractions, keep in mind that the product of multiplicative inverses is always equal to 1. Hence, we will can say that 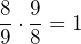 .
.
The following fraction word problems are great for practicing multiplication of fractions.
Example 5
John went to a shop and bought a pack of chocolates weighing 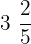 kg. A quarter of the chocolate packet contains chocolates with hazelnut toppings. What is the weight of hazelnut chocolates?
kg. A quarter of the chocolate packet contains chocolates with hazelnut toppings. What is the weight of hazelnut chocolates?
Solution
In this word problem we are given:
Total weight of all the chocolates = 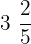 kg
kg
Number of chocolates with hazelnut toppings =  of the entire packet
of the entire packet
Weight of the chocolates with hazelnut toppings =  of
of 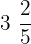 kg
kg
This means we have to multiply the two fractions to get the weight of the hazelnut chocolates. But, before multiplying, we will convert the weight of the entire chocolate packet into an improper fraction.
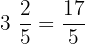
Weight of the chocolates with hazelnut toppings = 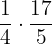 kg
kg
= 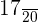 kg
kg
Hence, the weight of the chocolates with hazelnut toppings is 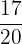 kg.
kg.
Example 6
Sam filled 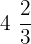 bottles of water. His friend John filled bottles
bottles of water. His friend John filled bottles 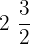 times as much as Sam. How many bottles of water did John fill?
times as much as Sam. How many bottles of water did John fill?
Solution
In this word problem we are given:
Fraction of bottles filled by Sam = 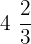 =
= 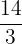
John filled bottles 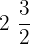 times as much as Sam. Convert this mixed fraction to an improper fraction like this:
times as much as Sam. Convert this mixed fraction to an improper fraction like this:
= 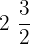 =
= 
Number of bottles filled by John = 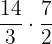
= 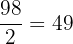
Hence, John fills 49 bottles.
Example 7
The favorite subject of  students in the class is mathematics. Out of these students,
students in the class is mathematics. Out of these students,  students are girls. What fraction of girls in a class like mathematics?
students are girls. What fraction of girls in a class like mathematics?
Solution
In this word problem we are given:
Fraction of students in a class who like mathematics = 
Fraction of girls who like mathematics =  of
of 
= 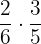
= 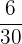
The fraction can be converted into a simplified form because both the numerator and the denominator are multiples of 6.
= 
Hence,  girls in the class like mathematics.
girls in the class like mathematics.












