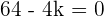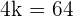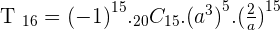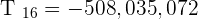Chapters

Exercise 1
Exercise 2
Exercise 3
Exercise 4
Exercise 5
Exercise 6
Exercise 7
Exercise 8
Exercise 9
Exercise 10

Develop the following binomials:

The best Maths tutors available

Exercise 1

1. $\text{[math]}$

$\text{[math]}$ $\text{[math]}$ $\text{[math]}$

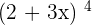
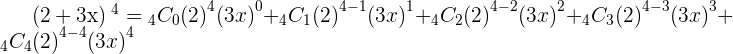
Exercise 2

2. $\text{[math]}$

$\text{[math]}$ $\text{[math]}$ $\text{[math]}$

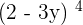
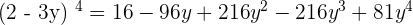
Exercise 3

3. $\text{[math]}$

$\text{[math]}$ $\text{[math]}$ $\text{[math]}$

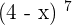
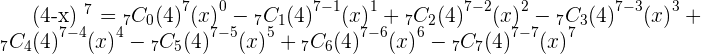
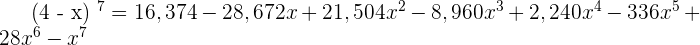
Exercise 4

4. $\text{[math]}$

$\text{[math]}$ $\text{[math]}$ $\text{[math]}$

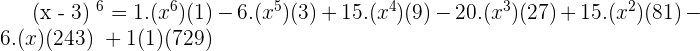
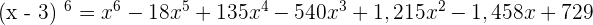
Exercise 5

4. $\text{[math]}$

$\text{[math]}$ $\text{[math]}$ $\text{[math]}$

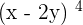
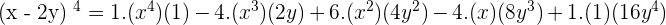
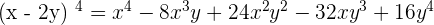
Exercise 6

Find the fifth term for the development of $\text{[math]}$ .

$\text{[math]}$ $\text{[math]}$ $\text{[math]}$

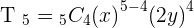
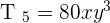
Exercise 7

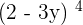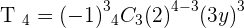
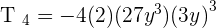
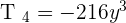
Calculate the fourth term for the development of $\text{[math]}$ .

$\text{[math]}$ $\text{[math]}$ $\text{[math]}$

Exercise 8

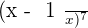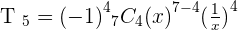
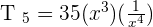
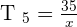
Calculate the fifth term for the development of $\text{[math]}$ .

$\text{[math]}$ $\text{[math]}$ $\text{[math]}$

Exercise 9

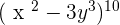
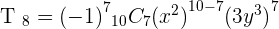
Find the eighth term for the development of $\text{[math]}$

$\text{[math]}$ $\text{[math]}$ $\text{[math]}$

Exercise 10

Find the independent term for the development of $\text{[math]}$ .

$\text{[math]}$

The exponent of a with the independent term is 0, therefore take only the literal part and equal it to $\text{[math]}$ .

$\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$

Did you like this article? Rate it!

4.00 (3 rating(s))

Emma

I am passionate about travelling and currently live and work in Paris. I like to spend my time reading, gardening, running, learning languages and exploring new places.

Binomial Theorem Worksheet

Exercise 1

Exercise 2

Exercise 3

Exercise 4

Exercise 5

Exercise 6

Exercise 7

Exercise 8

Exercise 9

Exercise 10

Theory

Dividing Algebraic Fractions

Operations with Monomials

Algebraic Identities

Monomials

Polynomial Roots

Factoring Polynomials

Dividing Polynomials

Algebraic Fractions

Adding or Subtracting Algebraic Fractions

Binomial Theorem

Adding Polynomials

Reducing Algebraic Fractions to a Common Denominator

Multiplying Polynomials

Algebraic Expressions

Remainder Theorem

Binomial Theorem

Multiplying Algebraic Fractions

Binimial Theorem Worksheet

Polynomials

Ruffini’s Rule

How to Solve Polynomials

Formulas

Binomial Formula

Polynomial Formulas

Algebra Formulas

Exercises

Algebraic Fractions Worksheet

Polynomial Worksheet

Factoring Polynomials Worksheet

Binomial Worksheet

Monomial Worksheets

Cancel reply