A polynomial is an algebraic expression having multiple terms. For example, the expression 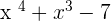 is a polynomial having 3 terms. It is also known as trinomial because it has 3 terms. Similarly,
is a polynomial having 3 terms. It is also known as trinomial because it has 3 terms. Similarly, 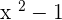 is a binomial expression because it has 2 terms. Binomials and trinomials are polynomial functions because they contain more than one term unlike monomials. A monomial is not a polynomial because it does not satisfy the basic definition of a polynomial.
is a binomial expression because it has 2 terms. Binomials and trinomials are polynomial functions because they contain more than one term unlike monomials. A monomial is not a polynomial because it does not satisfy the basic definition of a polynomial.
Adding and subtracting polynomials is easy because we just combine the like terms and apply the arithmetic operations of addition and subtraction. On the other hand, the division of polynomial can be tricky. We can divide two polynomials expressions either by using long division or by using synthetic division. In algebra, a long division method is used for dividing one polynomial by another. The polynomial which is a divisor in long division is either of the same degree or of the lower degree than the polynomial in the dividend.
Polynomial long division method can be done manually following step by step instructions and rules. The length of the division depends upon the degree of a polynomial.
The expression used to depict the outcome of the polynomial division is given below:
A = BQ + R
Here, A is the dividend, B is the divisor, Q and R are quotient and remainder respectively.
A polynomial yields a zero remainder if the divisor B is the factor of the dividend A. Before solving polynomial division problems, we need to arrange the polynomial function in the dividend in the descending order. In this article, we will discuss how to divide polynomials using the long division method through different examples. So, let us get started.

Example 1
Divide 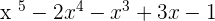 by
by  .
.
Solution
In the above division problem, 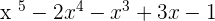 is the dividend and
is the dividend and  is the divisor. The highest degree of the polynomial is 5. We repeat the process in step 1 again and again until we reach the remainder.
is the divisor. The highest degree of the polynomial is 5. We repeat the process in step 1 again and again until we reach the remainder.
Follow these step by step instructions to divide the polynomials and find the quotient.
Step 1
- Write the polynomial in the form
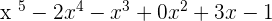
- We will start by dividing the first term of the dividend by the first term of the divisor.
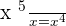 . Write this answer above at the quotient's place. It is the first term of the quotient.
. Write this answer above at the quotient's place. It is the first term of the quotient. - Now, we need to multiply
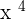 with the divisor
with the divisor  .
. 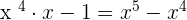 .
. - Subtract it from the dividend
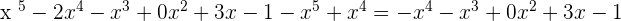 . This is the remaining part of the dividend.
. This is the remaining part of the dividend.
Step 2
- Divide the first term of the remaining dividend in the step 1 by the first term of the divisor.
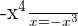 . Write this result in the quotient's place. This is the second term of the quotient.
. Write this result in the quotient's place. This is the second term of the quotient. - Now, multiplying
 by
by  will give us the following result.
will give us the following result.

- Subtract it from the remaining dividend.
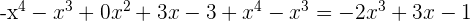 . This is the remaining part of the dividend.
. This is the remaining part of the dividend.
Step 3
- Divide the leading term of the remaining part of the dividend from step 2 by the first term of the divisor.
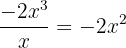 . Write it at the quotient's place. This is the third term of the quotient.
. Write it at the quotient's place. This is the third term of the quotient. - Multiply
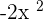 by the divisor
by the divisor  to get
to get 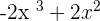 .
. - Subtract it from the remaining dividend
 . This is the remaining part of the dividend.
. This is the remaining part of the dividend.
Step 4
- Divide the first term of the remaining dividend in step 3 by the first term of the divisor.
 . Write it at the quotient's place. This is the fourth term of the quotient.
. Write it at the quotient's place. This is the fourth term of the quotient. - Multiply it with the divisor to obtain
 .
. - Subtract it from the remaining dividend to get
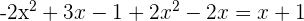 . This is the remaining part of the dividend.
. This is the remaining part of the dividend.
Step 5
- Divide the first term of the divisor by the first term of the remaining dividend.
 . Write this result at the quotient's place. This is the fifth term of the quotient.
. Write this result at the quotient's place. This is the fifth term of the quotient. - Multiply the divisor by 1 to get
 .
. - Subtract
 from the remaining dividend
from the remaining dividend  to get 0.
to get 0. - Hence, your division is complete.
Check for maths tuition here.
Remember that when a polynomial is completely divisible by another polynomial, then it means that the divisor is the factor of the dividend. In the above example,  is the factor of the polynomial
is the factor of the polynomial 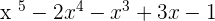 .
.

Example 2
Divide  by
by 
Solution
In the above example,  is the dividend and
is the dividend and  is the divisor. In other words, we can say that
is the divisor. In other words, we can say that  is the numerator and
is the numerator and  is the denominator. Follow these step by step instructions to obtain a quotient of the above example.
is the denominator. Follow these step by step instructions to obtain a quotient of the above example.
Step 1
- It is better to write the dividend as
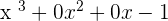 for your ease of calculation.
for your ease of calculation. - Divide the first term of the dividend by the first term of the divisor.
 . This will be the first term of the quotient.
. This will be the first term of the quotient. - Multiply
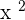 with the divisor
with the divisor  to get
to get 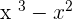 .
. - Subtract it from the dividend
 . This is the remaining dividend.
. This is the remaining dividend.
Step 2
- Divide the first term of the remaining dividend by the first term of the divisor.
 . This is the second term of the quotient.
. This is the second term of the quotient. - Multiply
 with
with  to get
to get 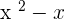 .
. - Subtract it from the remaining part of the dividend to get
 . We will cancel out
. We will cancel out 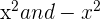 .
.  is the remaining part of the dividend in step 1.
is the remaining part of the dividend in step 1.
Step 3
- Divide the first term of the remaining dividend by the first term of the divisor.
 . This is the third term of the quotient.
. This is the third term of the quotient. - Multiply it with the divisor to get
 .
. - Subtract it from the remaining part of the dividend in step 2 to get 0.
Hence, our division is complete. Our quotient is 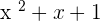 and our remainder is equal to 0 which means that the divisor in this example is the factor of the dividend.
and our remainder is equal to 0 which means that the divisor in this example is the factor of the dividend.
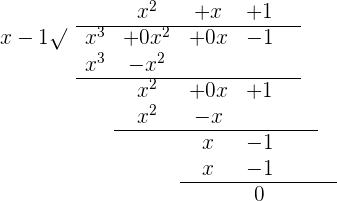
Example 3
Divide  by
by 
Solution
In the above example,  is the dividend and
is the dividend and  is the divisor. Follow these step by step instructions to solve the above example by polynomial long division method.
is the divisor. Follow these step by step instructions to solve the above example by polynomial long division method.
Step 1
- Divide the first term of the dividend by the first term of the divisor.
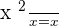 . This is the first term of the quotient.
. This is the first term of the quotient. - Multiply the divisor with this first term of the quotient to get
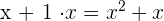 .
. - Subtract it from the dividend to get
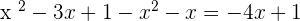 . This is the remaining part of the dividend.
. This is the remaining part of the dividend.
Step 2
- Divide the first term of the remaining dividend by the first term of the divisor.
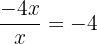 . This is the second term of the quotient.
. This is the second term of the quotient. - Multiply it by the divisor to get
 .
. - Subtract it from the remaining part of the dividend from the step 1.
 .
.
Hence, the division is complete because 5 cannot be further divided by the dividend. Hence, 5 is the remainder of this division. Since we did not get 0 as the remainder of this example, so it means that the divisor is not the factor of the dividend.

Example 4
Divide  by
by  .
.
Solution
In the above example,  is the dividend and
is the dividend and  is the divisor. Follow these step by step instructions to solve the above example through polynomial long division method.
is the divisor. Follow these step by step instructions to solve the above example through polynomial long division method.
Step 1
- Write the dividend as
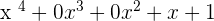 for the ease of your calculation.
for the ease of your calculation. - Divide the first term of the dividend by the first term of the divisor.
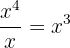 . This is the first term of the quotient.
. This is the first term of the quotient. - Multiply it by the divisor.
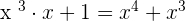 .
. - Subtract it from the dividend.
 . This is the remaining part of the dividend.
. This is the remaining part of the dividend.
Step 2
- Divide the first term of the remaining dividend in step 1 by the first term of the divisor.
 . This is the second term of the quotient.
. This is the second term of the quotient. - Multiply it by the divisor.
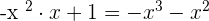 .
. - Subtract it from the remaining part of the dividend in the step 1.
 . This is the remaining part of the dividend.
. This is the remaining part of the dividend.
Step 3
- Divide the first term of the remaining dividend in step 2 by the first term of the divisor.
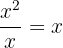 . This is the third term of the quotient.
. This is the third term of the quotient. - Multiply it by the divisor.
 .
. - Subtract it from the remaining part of the dividend in the step 2.
 .
.
The division will end here because 1 cannot be divided further by the divisor. Hence, 1 is the remainder of this example.

Example 5
Divide  by
by 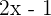 .
.
Solution
In the above example,  is the dividend and
is the dividend and 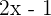 is the divisor. Follow these step by step instructions to solve this example by employing polynomial long division method.
is the divisor. Follow these step by step instructions to solve this example by employing polynomial long division method.
Solution
Step 1
- Divide the first term of the dividend by the first term of the divisor.
 . This is the first term of the quotient.
. This is the first term of the quotient. - Multiply it by the divisor.
 .
. - Subtract it from the dividend.
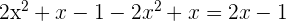 . This is the remaining part of the dividend.
. This is the remaining part of the dividend.
Step 2
- Divide the first part of the remaining dividend obtained in step 1 by the first term of the divisor.
 . This is the second term of the quotient.
. This is the second term of the quotient. - Multiply it by the divisor.
 .
. - Subtract it from the remaining part of the dividend from step 1 to get 0.
Hence, the division is complete. Remember that when a polynomial is completely divisible by another polynomial, then it means that the divisor is the factor of the dividend. In the above example, 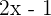 is the factor of the polynomial
is the factor of the polynomial  .
.
Summarise with AI:













