Chapters

What is the Binomial Theorem?
The word Binomial can be broken into two. Bi means two and nomial mean mathematical term. If we add them together that means an algebraic expression with 2 terms only. If you are wondering why algebraic expression? Then imagine a non-algebraic expression, for example,  . You can easily solve it, just add both numbers and then multiply itself for 4 times (since the exponent is 4) and you will get 4096 as your answer. However, if we imagine algebraic expression, for example,
. You can easily solve it, just add both numbers and then multiply itself for 4 times (since the exponent is 4) and you will get 4096 as your answer. However, if we imagine algebraic expression, for example,  , it is not that simple. You need to expand the equation or expression.
, it is not that simple. You need to expand the equation or expression.
The binomial theorem states that the sum of two numbers (let's just say x and y) with the exponent as a positive integer then it will be expressed as the sum of 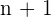 terms of the form where n is the exponent. We use binomial when we need to expand the expression with high power such as
terms of the form where n is the exponent. We use binomial when we need to expand the expression with high power such as 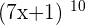 . However, the binomial theorem has only two limitations.
. However, the binomial theorem has only two limitations.
- The power should be positive,
- The power should be in whole numbers.
If the above limitations don't fulfill then you can't use the binomial formula. To solve those expressions, we use a different technique which we will discuss later. The expression of the binomial theorem is:

where:
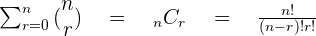
 is the exponent of the expression
is the exponent of the expression
 is the number of terms
is the number of terms
Factorial Notation
In order to use the combination, you need to understand factorial notation. If you are using a scientific calculator then you will have no problem. Just input the n and r values and you will get your answer. However, if you are not using a scientific calculator then you need to use factorial notation to find the combination value. If you see any number with an exclamation mark (e.g 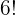 ) that means you need to expand it with the help of factorial notation. Below is the way to expand the factorial notation:
) that means you need to expand it with the help of factorial notation. Below is the way to expand the factorial notation:

You can also use pascal's triangle to find out the value. Pascal's triangle method is one of the oldest methods to find the factorial of a number.
Pascal's Triangle
This method was invented by a famous French mathematician. His name is Blaise Pascal (1623 - 1662) and he made a triangular array in which numbers were added in adjacent elements in preceding rows. Here is a small example of Pascal's Triangle.
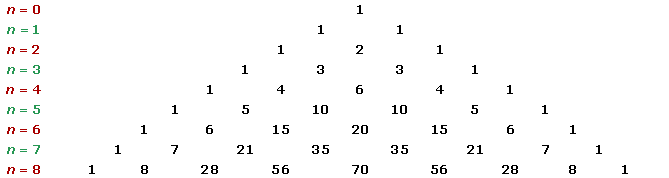
The triangle doesn't end till n=8. As a matter of fact, it keeps on going to infinity. Let's break the triangle into rows. The first row will be known as 0th Row (i.e. 1) and the second row will be known as 1st Row (i.e. 1,1). Each row will be numbered according to this pattern. The reason for numbering the rows is that it indicates the exponent. For example, your question is  and you want to find the coefficient value of the 3rd term. This means that you need to find the 2nd Row term. If you are wondering why 2nd Row then remember the first row is called 0th Row and if we count from 0 then the third term will be 2.
and you want to find the coefficient value of the 3rd term. This means that you need to find the 2nd Row term. If you are wondering why 2nd Row then remember the first row is called 0th Row and if we count from 0 then the third term will be 2.
Combination Method
One of the easiest methods to find the coefficient of the terms is the combination method. The formula of combination is:
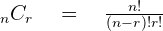
 is the exponent of the expression
is the exponent of the expression
 is the number of terms
is the number of terms
Let's take the above example of  , you need to find the 3rd term. This means that the value of n is 5 and since you need to find the 3rd term, therefore, r will be 3. This will be written as:
, you need to find the 3rd term. This means that the value of n is 5 and since you need to find the 3rd term, therefore, r will be 3. This will be written as:
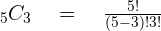
Use the factorial notation formula to expand the expression so that you can further simplify it.
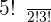
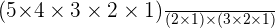
Cancel out " " and the remaining will be:
" and the remaining will be:
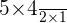

So your third term will be "10". This might look easy however in real life it isn't. You will be getting high values such as 10, 20, 25, etc. If you start using this formula, it will take you days to find all the terms. Not to forget that a little error can create a lot of mess. You can find this value directly from calculators. Do note that you can only find coefficients from scientific calculators only. If you are using a calculator, you can find any value in just a few seconds with 100% accuracy. All you need to do is to plug in the value of n and r and your calculator will find the value. Make sure that you entered the correct value of n and r.
Check for maths tuition here.
Examples
1. 
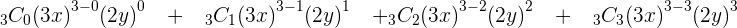
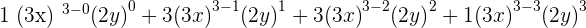
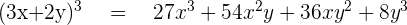
2. 
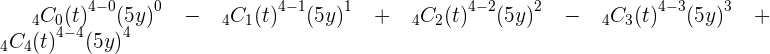
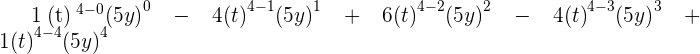

3. 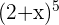



Summarise with AI:













