In algebra, algebraic fractions are the fractions that have algebraic expressions (the expressions which have one or more variables and arithmetic operations) both in the numerator and the denominator.
We can apply the operations of addition, subtraction, multiplication, and division on these algebraic fractions, just like we apply on common fractions. Adding and subtracting fractions is simple as we just need to take the LCM (Least Common Multiple) of both denominators. For fractions, this LCM is also known as LCD (Least Common Denominator or Lowest Common Denominator).
We multiply or divide algebraic expressions just like we multiply or divide the common fractions. Diving fractions means that we will take the reciprocal of the fraction written after the "division" sign and solve the remaining expression for the multiplication operation. In this article, we will only discuss how to multiply two algebraic fractions together along with the relevant examples.
Before proceeding to example, let us first see how to multiply two algebraic fractions together.
 and
and  are two algebraic fractions. When both these fractions are multiplied together we will get the following new algebraic fraction:
are two algebraic fractions. When both these fractions are multiplied together we will get the following new algebraic fraction: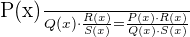

Example 1
Multiply the following algebraic fractions:
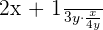
Solution
In this examples, we are given two simple fractions. We will multiply the numerators and denominators together.

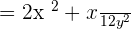
The last step of the multiplication is to check whether there is a common factor in the numerator or denominator. We cancel out the common factor to simplify the answer further. In the above answer, there is no common factor in the numerator and the denominator, so we have left the answer as it is.
Example 2
Multiply the following algebraic fractions:
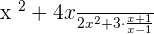
Solution
When two algebraic expressions with same variables are multiplied together, then we add the powers of those variables in the resultant expression.

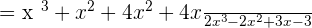
Now, we will simplify the fractions by adding or subtracting the like terms together:
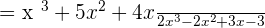
Example 3
Multiply the following algebraic fractions:
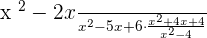
Solution
You can notice that some expressions in the numerator and the denominator can be factorized:
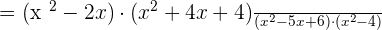
After the factorization of the polynomial 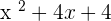 , we will get
, we will get 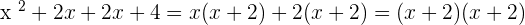
After the factorization of the polynomial  , we will get
, we will get 
We will expand the terms in the numerator and the denominator by writing their factors instead of the entire polynomial expression:

The same factors in the numerator and the denominator will be canceled out. We will write the final answer in the most simplified form like this:

Find the best Maths tutor on Superprof.
Example 4
Multiply the following algebraic fractions together:
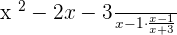
Solution
The numerator will be multiplied with the numerator and the denominator with the denominator. We can write the above expression like this:

The algebraic expression 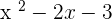 can be factorized like this:
can be factorized like this:
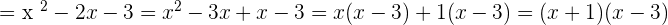
You can see that we have written the factorized form as a product of two binomial expressions.
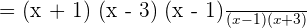
We will cancel out the like terms together and write the final answer in the most simplified form like this:
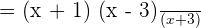
Find more Maths tutor here on Superprof.
Example 5
Multiply the following algebraic fractions together:

Solution
We will multiply the expressions in the numerator and denominator together. As we know that when like terms ( terms having same variables) are multiplied together, their powers or exponents are summed up. Both fractions have same denominator, so we have taken the square of the denominator instead of writing it twice or multiplying it using the long procedure.
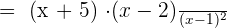

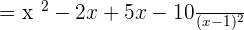
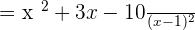
Example 6
Multiply the following algebraic fractions together:

Solution
In this example, we are given the expressions containing more than one variables. When expressions with same variables are multiplied together, the resultant expression has exponent equal to the sum of the exponents of expressions that are multiplied together. However, when different variables are multiplied with each other, their exponents are not summed up.


For simplifying, we will add the like terms together:
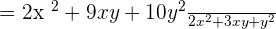
Example 7
Multiply the following algebraic fractions together:

Solutions
Both fractions have common denominators:


Add the like terms together:
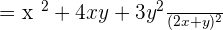
Example 8
Multiply the following algebraic fractions together:

Solution
We know that 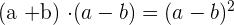 . After multiplication, we will write the resultant expression as
. After multiplication, we will write the resultant expression as 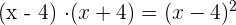 .
.




Summarise with AI:













