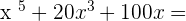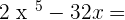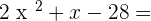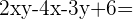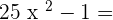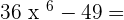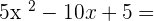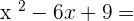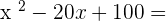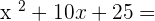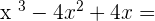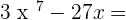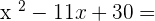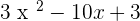Chapters
- Factor and Calculate the Roots of the Following Polynomials
- Exercise 1
- Exercise 2
- Exercise 3
- Exercise 4
- Exercise 5
- Exercise 6
- Exercise 7
- Exercise 8
- Exercise 9
- Exercise 10
- Exercise 11
- Exercise 12
- Exercise 13
- Exercise 14
- Exercise 15
- Solution of exercise 1
- Solution of exercise 2
- Solution of exercise 3
- Solution of exercise 4
- Solution of exercise 5
- Solution of exercise 6
- Solution of exercise 7
- Solution of exercise 8
- Solution of exercise 9
- Solution of exercise 10
- Solution of exercise 11
- Solution of exercise 12
- Solution of exercise 13
- Solution of exercise 14
- Solution of exercise 15

The best Maths tutors available
Factor and Calculate the Roots of the Following Polynomials
Exercise 1
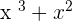
Exercise 2

Exercise 3
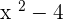
Exercise 4
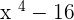
Exercise 5

Exercise 6

Exercise 7

Exercise 8
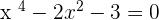
Exercise 9

Exercise 10
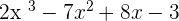
Exercise 11

Exercise 12
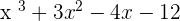
Exercise 13
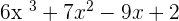
Exercise 14
Factorize the following.
Exercise 15
Factorize the following.
Solution of exercise 1
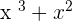
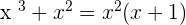
Solution of exercise 2

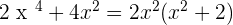
Solution of exercise 3
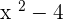
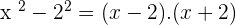
Solution of exercise 4
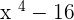
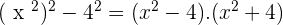
Solution of exercise 5


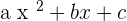
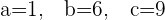
In order to break the middle term, you need to multiply "a" with "c":

Now break 9 into least possible factors:
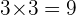
The next step is to check the sign of the c and in this case, it is positive this means that you need to add the factors to come up with 6:
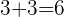
Now your middle term is broken, you can carry forward:



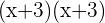

Solution of exercise 6

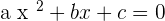
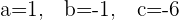
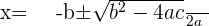
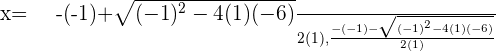
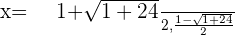


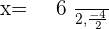

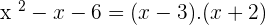
Solution of exercise 7

Assuming  :
:
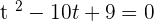
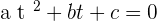
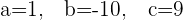
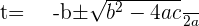
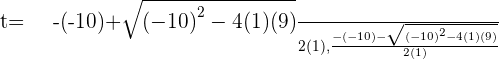

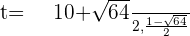
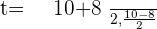
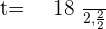

Putting the value of t:


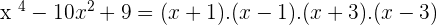
Solution of exercise 8
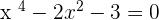
Assuming  :
:

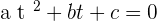
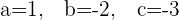
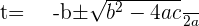
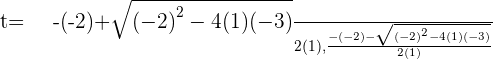
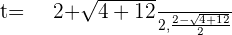
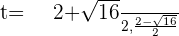

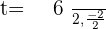

Putting the value of t:
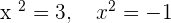
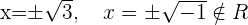
Solution of exercise 9
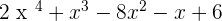
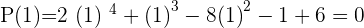
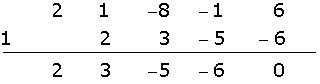
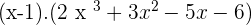
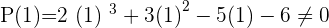
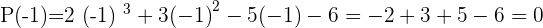


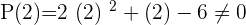
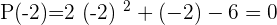
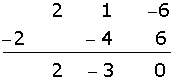
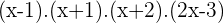
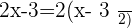
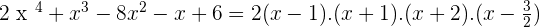
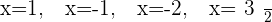
Solution of exercise 10

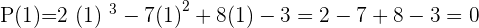
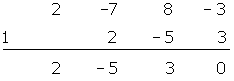
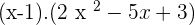

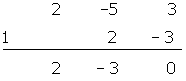
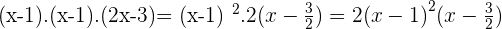
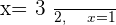
Solution of exercise 11

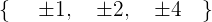
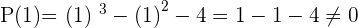

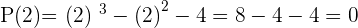
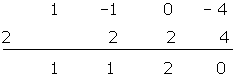

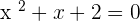
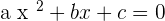
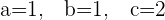
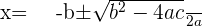
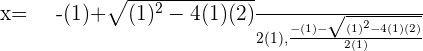
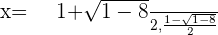
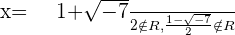


Solution of exercise 12
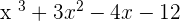


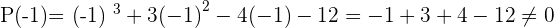
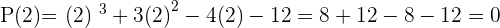
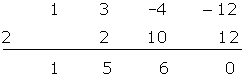
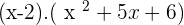

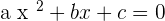
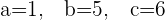
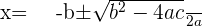
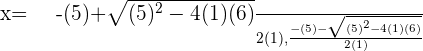

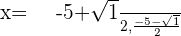

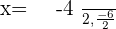

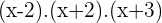

Solution of exercise 13
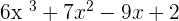


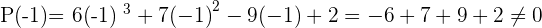
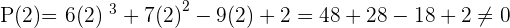
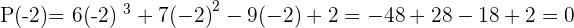

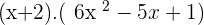
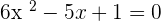
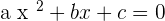
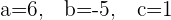
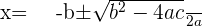
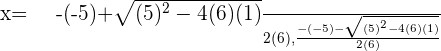
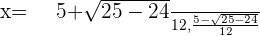
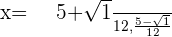
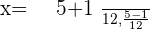
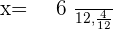
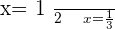


Solution of exercise 14


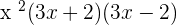



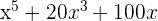
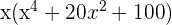
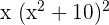


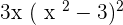


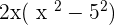
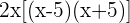
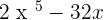
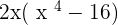
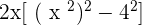
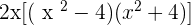
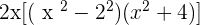
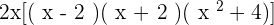

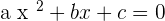

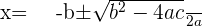

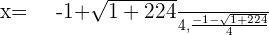

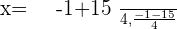

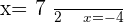
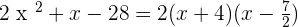
Solution of exercise 15
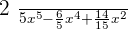
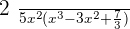
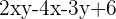

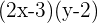


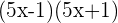

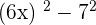

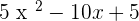
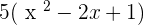
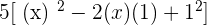
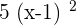
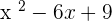

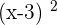
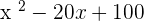
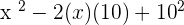
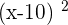


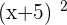
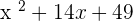
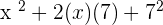

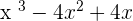
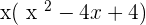
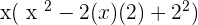
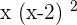
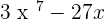

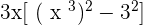

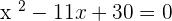


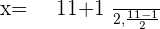



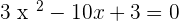
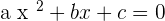
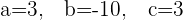
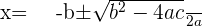
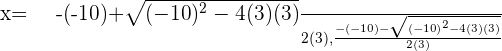

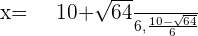
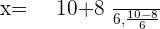
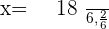

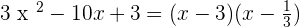
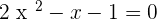
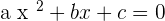

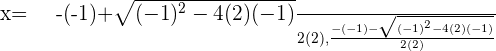
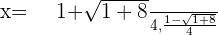
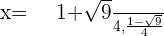
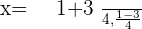

Summarise with AI: