Chapters
Algebraic identities are algebraic equations that are true for all the variables present in them. These identities contain constants and variables on both sides of the equation. When we factorize a polynomial, we often use these algebraic identities. A polynomial function is an algebraic expression that contains more than one term. Examples of polynomials include binomials and trinomials.
Quadratic equations are also the form of polynomial functions because they contain 3 terms. The highest exponent in a quadratic function is 2 and its graph is a parabola, unlike linear equation. Linear equations are graphically represented by a straight line. You might have learned these algebraic identities in junior classes when studying basic algebra because the uses of these identities are widespread while solving equations.
You can use the substitution method to verify the algebraic identities. The substitution method means substituting any value of the variable on both sides of the algebraic identity. If you have correctly expanded or solved an example using algebraic identities, then any value of the variable will hold true for both the left and right hand side of the equation.
In this article, we will see some standard algebraic identities and their relevant examples.
Find good maths tutors near me here.

Square of a Binomial
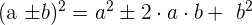
The above algebraic identity is also known as a quadratic identity because after expansion and setting the equation equal to zero, we get a quadratic formula. The sign with 2ab will depend upon the addition and subtraction sign between a and b.
Using the above algebraic identity, we will solve some examples. You will see that any value of the variable satisfied both sides of the equation.
Example 1

Use the algebraic identity 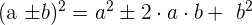 to open up the parentheses of this question.
to open up the parentheses of this question.

Since, there is a positive sign between  and 3, so we will use a positive sign with
and 3, so we will use a positive sign with  .
.
= 
The answer 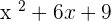 is also a quadratic equation since the standard form of a quadratic equation is
is also a quadratic equation since the standard form of a quadratic equation is 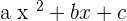 . In this answer, the leading coefficient
. In this answer, the leading coefficient 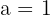 , the middle coefficient
, the middle coefficient  and the last constant term
and the last constant term  . The last term of the quadratics is a constant term in which no variable is involved.
. The last term of the quadratics is a constant term in which no variable is involved.
Hence,  . It means that all the variables hold true for both sides of this algebraic equation.
. It means that all the variables hold true for both sides of this algebraic equation.
Example 2

Use the algebraic identity 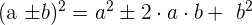 to open up the brackets of this question.
to open up the brackets of this question.
=
Since there is a negative sign between  and 3, so we will expand it by subtracting the middle term
and 3, so we will expand it by subtracting the middle term 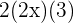 :
:
= 
Hence, 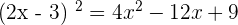 . It means that all the variables hold true for both sides of the equation.
. It means that all the variables hold true for both sides of the equation.
Example 3
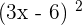
Use the algebraic identity 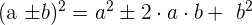 to solve this equality:
to solve this equality:
=
Since there is a negative sign between  and 6, so we will use a negative sign with the middle term
and 6, so we will use a negative sign with the middle term  :
:
=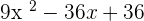
Hence, 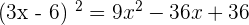 , which means that all the variables hold true for both sides of this equality.
, which means that all the variables hold true for both sides of this equality.
Difference of Squares
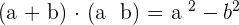
It means that the multiplication of the terms 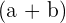 and
and  will give us
will give us  . Let us solve some examples related to this identity:
. Let us solve some examples related to this identity:
Example 1
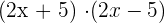
Use the algebraic identity 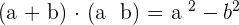 to solve this example:
to solve this example:
= 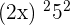
= 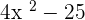
Hence,  .
.
Example 2

Use the algebraic identity 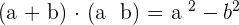 to solve this example:
to solve this example:
=
=
Hence, 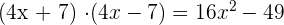 .
.
Cube of a Binomial
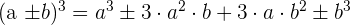
Example 1
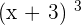
Use the algebraic identity 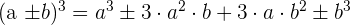 to solve this example:
to solve this example:

Since there is a positive sign between  and 3, so we will use a positive sign with
and 3, so we will use a positive sign with  and
and  while solving the above expression.
while solving the above expression.
= 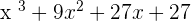
Hence, 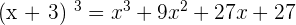 .
.
Example 2

Use the algebraic identity 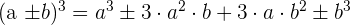 to solve this example:
to solve this example:
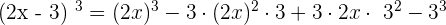
Since there is a negative sign between  and 3, hence we will use a negative sign with
and 3, hence we will use a negative sign with  and
and  .
.
= 
Hence, 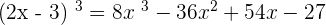 .
.
Square of a Trinomial

Example 1
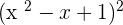
Use the algebraic identity  to solve this example:
to solve this example:
=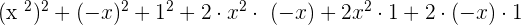
= 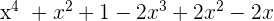
=
Hence, 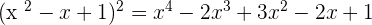 .
.
Example 2

Use the algebraic identity  to solve this example:
to solve this example:
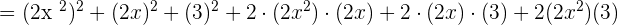

Hence,  .
.
Sum of Cubes

It means that multiplying 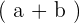 and
and 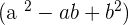 will give an expression
will give an expression 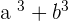 . Lets us consider the following examples related to this algebraic identity.
. Lets us consider the following examples related to this algebraic identity.
Example 1

Use the algebraic identity  to solve this problem:
to solve this problem:
=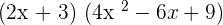
Hence,  .
.
Example 2

Use the algebraic identity  to solve this problem:
to solve this problem:
= 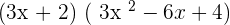
Hence, 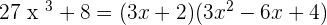 .
.
Difference of Cubes
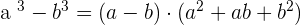
Consider the following examples related to this algebraic identity.
Example 1

Since  and 27 are perfect cubes, therefore we will use the algebraic identity
and 27 are perfect cubes, therefore we will use the algebraic identity 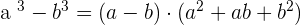 to solve this problem:
to solve this problem:
= 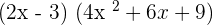
Hence, 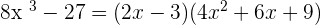 .
.
Example 2

Since 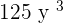 and 8 are perfect cubes, therefore we will use the algebraic identity
and 8 are perfect cubes, therefore we will use the algebraic identity 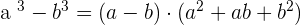 to solve this problem:
to solve this problem:

Hence, 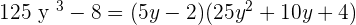 .
.
Special Algebraic Identity
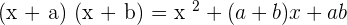
It means that whenever the question of the form 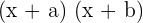 will be multiplied together we will get
will be multiplied together we will get 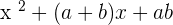 . Consider the following examples related to this algebraic identity:
. Consider the following examples related to this algebraic identity:
Example 1

Use the algebraic identity 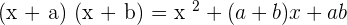 to solve this problem:
to solve this problem:
=
= 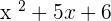
Hence,  .
.
Example 2

To simplify, use the algebraic identity 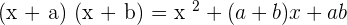 to solve this problem:
to solve this problem:
= 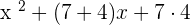
= 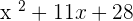
Hence,  .
.
Factorization with Algebraic Identities
So far, we have seen the algebraic identities and their respective examples. Now, we will see how to solve equations by expanding or factoring the algebraic expressions using algebraic identities.
Example 1
 using standard algebraic identities.
using standard algebraic identities. Solution
In the above example,  and
and  .
.
We will use  to factorize the expression in this problem. Since,
to factorize the expression in this problem. Since,  and
and  , so we will write the expression as follows in the factored form:
, so we will write the expression as follows in the factored form:
= 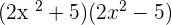
Example 2
Expand 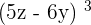 using a standard algebraic identity.
using a standard algebraic identity.
Solution
Use 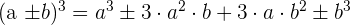 to expand the above question:
to expand the above question:
In this example,  and
and 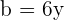 . Hence, using the above formula, we will write this expression as:
. Hence, using the above formula, we will write this expression as:

Since there was a negative sign between  and
and 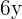 , hence we will subtract
, hence we will subtract 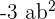 while expanding the formula:
while expanding the formula:

Example 3
Find the product of  using standard algebraic identity.
using standard algebraic identity.
Solution
For simplifying, use the algebraic identity 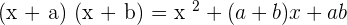 to solve this problem:
to solve this problem:


Summarise with AI:













