Chapters

What Does Algebraic Expression Mean?
In the world of mathematics, you will encounter algebraic equations or expressions. Before we start to solve Algebraic equations or expressions, we should know what it means. Algebra is the handling of numerical relations in which one or more quantities are unknown. These terms are called variables or unknowns and they are represented by letters. However, an algebraic expression is an expression that contains variables as well as constant with algebraic operations (which are +,-,x, and ÷). Below is an example of an algebraic expression:

Where,
 and
and  are the variables,
are the variables,
 is the coefficient,
is the coefficient,
 is the constant,
is the constant,
and - and + are the algebraic operators.
An algebraic expression can be in any form. The key point is that every algebraic expression contains a variable as well as algebraic operation. You can't construct an algebraic equation or expression without variables. However, coefficients and constants aren't necessary to construct an algebraic expression. In simple words, you can still make an algebraic equation or expression without constant and coefficient. Below is an example of an algebraic expression without coefficient and constant:

As you can see it contains variables only with algebraic operations. It doesn't matter we know the values of the variables or not, we can declare this expression as an algebraic expression. Let's further dive into the components of algebraic expression.
Variable
Variable is the heart of the algebraic equation and expression. Remember, it is necessary for an algebraic equation and expression to have variables otherwise you can't call it algebraic equation or expression (as discussed above). Variables are represented by letters, you will mostly see "x" and "y" as variables but this doesn't mean that you can't use other letters. You can use any alphabet you want.
Variable is the disguise number which you need to find in an algebraic equation or expression. In some cases, variables can have more than one answer that is why we call it variable since it can vary (we will discuss it later in Quadratic Equations).
Coefficient
A coefficient is a number beside the variable. Every variable has a coefficient. For example, you are given this algebraic expression "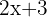 ". The coefficient is 2, how did we know that? As mentioned above, a coefficient is a number beside variable then look at the variable first. What is beside the variable? It is 2, therefore we can say that the coefficient of algebraic expression "
". The coefficient is 2, how did we know that? As mentioned above, a coefficient is a number beside variable then look at the variable first. What is beside the variable? It is 2, therefore we can say that the coefficient of algebraic expression "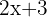 " is "2". Test yourself, here is an algebraic expression"
" is "2". Test yourself, here is an algebraic expression"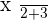 ", what is the coefficient? If your answer is
", what is the coefficient? If your answer is  then you are correct!
then you are correct!
Let's take another example, your teacher asked you to find the coefficient of this algebraic expression,"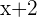 ". As you can see there is no number before x so this means that there is no coefficient? No, there is a coefficient but it is hidden. Let's rewrite this expression and it will be, "
". As you can see there is no number before x so this means that there is no coefficient? No, there is a coefficient but it is hidden. Let's rewrite this expression and it will be, " ". Now can you see the coefficient? Yes! It is "1" but how did we find out? When there is no coefficient written before a variable that means there is 1 by default. We don't write 1 with every variable because it is obvious. Don't forget that every variable has a coefficient.
". Now can you see the coefficient? Yes! It is "1" but how did we find out? When there is no coefficient written before a variable that means there is 1 by default. We don't write 1 with every variable because it is obvious. Don't forget that every variable has a coefficient.
Constant
Constant is a number that is either added or subtracted from a variable. Constant isn't an important part of an algebraic equation and expression. This means an algebraic equation or expression can survive without a constant. However, the answer will vary if you remove or add the constant. For example, in this algebraic expression(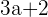 ), you were given a=3. The answer will be 11 but you accidentally forgot to add the constant, now the answer will be 9. In conclusion, you can create an algebraic equation or expression without a constant but it won't be accurate (if you forgot to add or subtract the constant).
), you were given a=3. The answer will be 11 but you accidentally forgot to add the constant, now the answer will be 9. In conclusion, you can create an algebraic equation or expression without a constant but it won't be accurate (if you forgot to add or subtract the constant).
Find good maths tutors near me here.
Algebraic Expression Used in Geometry
The algebraic expressions also help us in Geometry. As a matter of fact, all Geometrical shape's area, perimeter, and volume formulas are algebraic expressions. Imagine a circle,
Length of the circumference: L = 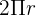 , where r is the radius of the circumference.
, where r is the radius of the circumference.
Area of the square: S = 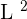 , where L is the side of the square.
, where L is the side of the square.
Volume of the cube: V = 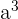 , where a is the edge of the cube.
, where a is the edge of the cube.
Common Algebraic Expressions
The double of a number: 2x
The triple of a number: 3x
The quadruple of a number: 4x
Half of a number: x/2.
A third of a number: x/3.
A quarter of a number: x/4.
A number is proportional to 2, 3, 4, ...: 2x, 3x, 4x,...
A number to the square: x²
A number to the cube: x³
Two consecutive numbers: x and x + 1.
Two consecutive even numbers: 2x and 2x + 2.
Two consecutive odd numbers: 2x + 1 and 2x + 3.
Break 24 in two parts: x and 24 − x.
The sum of the two numbers is 24: x and 24 − x.
The difference of two numbers is 24: x and 24 + x.
The product of two numbers is 24: x and 24/x.
The quotient of two numbers is 24; x and 24 · x.
Numerical Value of an Algebraic Expression
The numerical value of an algebraic expression for a particular value is the number obtained by replacing the unknown values with the numerical value given and perform the operations.
L(r) = 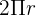
r = 5 cm L (5)= 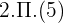 = 78.54 cm²
= 78.54 cm²
S(L) =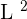
L = 5 cm A(5) =  = 25 cm²
= 25 cm²
V(a) = 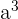
a = 5 cm V(5) = 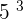 = 125 cm³
= 125 cm³
Types of Algebraic Expressions
Monomial
A monomial is an algebraic expression formed by a single term.
Binomial
A binomial is an algebraic expression formed by two terms.
Trinomial
A trinomial is an algebraic expression formed by three terms.
Polynomial
A polynomial is an algebraic expression consists of more than one term.













