In algebra, a binomial is a polynomial with exactly two terms, such as (a + b). Expanding binomials—specifically squaring or cubing them—is a fundamental skill used to simplify complex equations.
Instead of multiplying the brackets manually every time, we use specific patterns known as Special Products to find the answer quickly.
Key Formulas:
Square of a Sum:
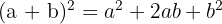
Square of a Difference:
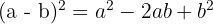
Cube of a Sum:
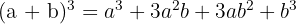
Cube of a Difference:


The best Maths tutors available
Worked Example
Expand the following expression:
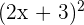
Solution: Here, a = 2x and b = 3. We use the Square of a Sum formula.
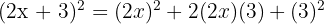
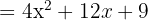
Practice Questions & Solutions
1
Expand:
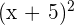
Solution
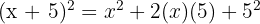
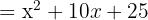
2
Expand:
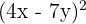
Solution
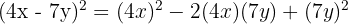
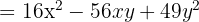
3
Expand:
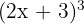
Solution
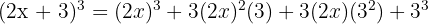
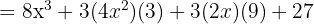
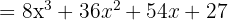
4
Expand:
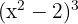
Solution
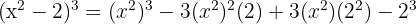
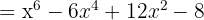
5
Expand:
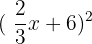
Solution
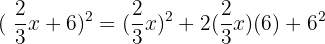
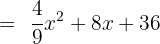
6
Expand:
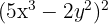
Solution
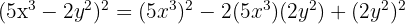
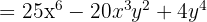
7
Expand:
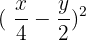
Solution
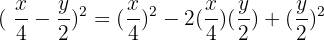
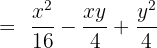
8
Expand:
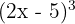
Solution
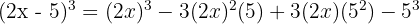
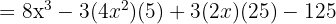
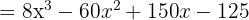
9
Expand:
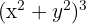
Solution
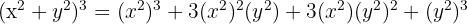
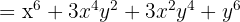
10
Expand:
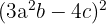
Solution
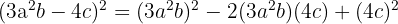
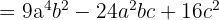
Summarise with AI:












