Chapters

What is Algebra?
The word algebra came from the Arabic language (al-jebr) which means "reunion of broken parts". It is one of the parts of mathematics which deals with symbols, relations, and manipulation of symbols. The symbols (which you might find written in Greek or Latin language) represents quantities that don't have a fix value or values. We call them variables since they can vary. There are sub-branches of Algebra as well, they are Geometry, Calculus, and Arithmetic.
How To Add Algebraic Fractions?
Adding algebraic fractions is almost as same as adding number fractions. However, you need to apply all the algebraic rules in order to add all the algebraic functions. When you encounter algebraic fractions, the first thing you need to find is either the denominators are the same or not?
Adding or Subtracting Algebraic Fractions with the Same Denominator
In simple words, since the denominators are the same, all you need to do is add or subtract the numerators. Pretty simple, right? Let's do an example.
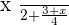
Remember to check the denominator first! Check the above example, do you think the denominators are the same? Of course no! One fraction contains 2 as the denominator while the other fraction contains 4 as the denominator. Therefore, we can conclude that denominators aren't the same. Does that mean we can't solve it? No, there is nothing as impossible in maths! We can solve it but later, right now we are focusing on adding fractions with the same denominators. Look at the expression below:
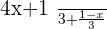
Now check the denominators again. Are both denominators the same? Yes, both denominators are 3 therefore, we can proceed with adding the numerators. Now it will become simple algebraic manipulation.
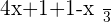
Separating all the numbers and variables to make easier and clear. Furthermore, it reduces the chances of errors.
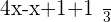
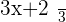
You might be thinking this is the answer. Yes, you are correct but it doesn't look good because we can simplify it more.
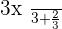
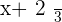
It doesn't matter how many fractions are there until the denominator is the same then all you need to do is to add or subtract the numerator according to the sign.
Examples
Example No.1: 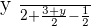
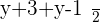
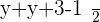
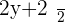
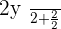
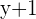
Example No.2: 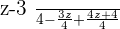
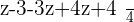
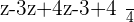
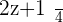
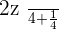

Example No.3: 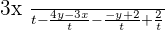

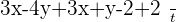
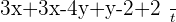

Find a good maths tutor near me here.
Adding or Subtracting Algebraic Fractions with Different Denominators
Adding or subtracting algebraic fractions with different denominators might be little bit tricky. The first part is to make the denominators same. Do note that making denominators same is important otherwise you can't add or substract numerators. In order to make the denominators same, you need to take LCM.
LCM means Least Common Factor. You need to multiply all the numerators and denominators with a number which is the least common factor. The least common factor is a positive integer which will make all the denominators equal.
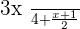
What was the first step? To check the denominator. Both denominators are different therefore we need the least common multiple to make them equal. If I multiply the second fraction with 2 in the denominator than both denominators can be equal. However, if I am multiplying the denominator with 2 then according to mathematics principle, I need to multiply the numerator with 2 as well.
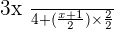
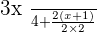
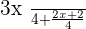
Now the denominators are the same, we can carry out the addition or subtraction of numerators.
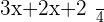
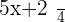
What if the denominator is not a number but instead it is a variable? Then we need to change our method of finding the least common multiple. However, you still need to find the least common multiple but with a different approach.
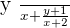
In the above example, we find that both denominators are not equal. Furthermore, we also find that denominators contain variables. The best way to make both denominators equal is to multiply the denominators with each other. Do remember that when you are multiplying something with the denominator, you need to multiply it with numerator as well.
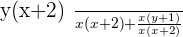
So I multiplied the first fraction's denominator with the second fraction's denominator. Just like that, I multiplied the second fraction's denominator with the first fraction's denominator. Now as you can see both denominators are equal to each other which means now you can add or subtract the numerators without any hurdles.
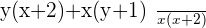
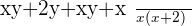
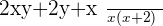
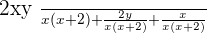
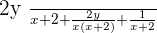
This is how you solve algebraic fractions. Below are more examples of algebraic fractions (with different denominators).
Example No.1: 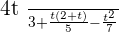

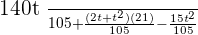
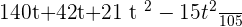
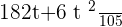
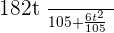
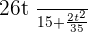
Example No.2: 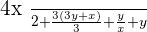 (When there is nothing written in denominator than it means denominator is equal to "1")
(When there is nothing written in denominator than it means denominator is equal to "1")
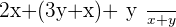 (Always be the smartest in the room. If you notice the numerators were divisible by denominators.)
(Always be the smartest in the room. If you notice the numerators were divisible by denominators.)
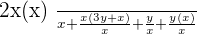
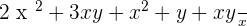
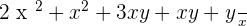
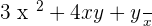
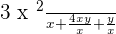
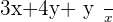
Example No.3: 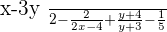
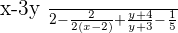
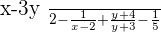
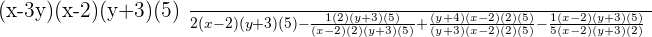
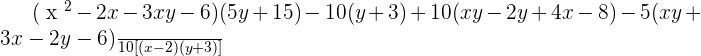
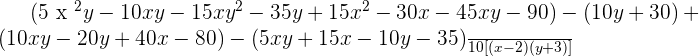
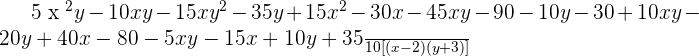
Rearranging the above expression:


Taking out 5 as a common factor in numerator:


Summarise with AI:













