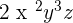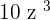Chapters
In algebra, a monomial can be defined in a variety of ways. The most common definition is:
"A monomial is an algebraic expression having a single term only."
Another definition of a monomial is
"A monomial is an algebraic expression in which the only operations that appear between the variables are the product and the power of the natural exponent."
The opposite of monomial is a polynomial. As the name implies, a polynomial is an algebraic expression that contains multiple terms. Binomials and trinomials are examples of polynomials functions. A binomial has two terms whereas a trinomial has three terms.

Examples of Monomials
The following algebraic expressions have a single term only and are also the product of constants and variables. Hence, they satisfy both the above definitions of the monomial terms.
Rules of Monomials
You should keep in mind the following two rules of monomials:
- When a monomial is multiplied by a constant, we get another monomial.
- A monomial cannot have negative or fractional exponents. In other words, we can say that the exponent of a monomial term should be a non zero whole number.
For example, the terms 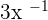 ,
, 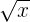 and
and 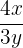 are not monomials because their exponents are negative or fractional.
are not monomials because their exponents are negative or fractional.
The following table shows algebraic expressions that are monomial and not a monomial.
| Expression | Monomial / Not a monomial |
|---|---|
| Monomial | |
| Not a monomial | |
| Monomial | |
| Monomial | |
| Not a Monomial |
You can see in the above table that the first, third and fourth expressions are monomials because they have a single term and they have non negative exponents. On the other hand, second and fifth expressions are not monomials because the second term has a negative exponent and the fifth term has a fractional exponent.
Parts of a Monomial
A monomial has three parts, a coefficient, a literal part, and a degree. All these parts are explained below in detail.
Coefficient
The coefficient of a monomial is the number that multiplies the variable(s). In other words, we can say that when any constant is multiplied by the variable, it becomes a coefficient. Consider the following examples of coefficients:
Examples
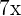 means 7 times x. In this expression,
means 7 times x. In this expression,  is a variable and 7 is a coefficient.
is a variable and 7 is a coefficient.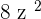 means 8 times
means 8 times  square. In this expression,
square. In this expression,  is a variable and 8 is a coefficient.
is a variable and 8 is a coefficient. means 9 times
means 9 times  cube. In this expression,
cube. In this expression,  is a variable and 9 is a coefficient.
is a variable and 9 is a coefficient.
A variable with no constant with it has a coefficient of 1. For example, 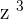 ,
, 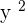 and
and  all are monomials having a coefficient of 1.
all are monomials having a coefficient of 1.
Literal Part
The literal part is constituted by the letters and its exponents. Exponents are also known as powers on indices. For example, the exponent of  is 3 and the exponent of
is 3 and the exponent of 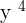 is 4. Let us explain this concept further through the following examples.
is 4. Let us explain this concept further through the following examples.
Examples
- In the monomial term
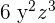 , the literal part is
, the literal part is  because it contains letters and numbers.
because it contains letters and numbers. - In the monomial term
 , the literal part is
, the literal part is  .
. - The monomial expression
 has the literal part
has the literal part 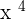 .
.
Degree
The degree of a monomial is the sum of all exponents of the letters or variables.
For example, the degree of 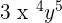 is 10. The constant has a degree equal to one.
is 10. The constant has a degree equal to one.
Do not confuse the degree of a monomial with the highest degree. The degree of a monomial is the sum of the degree of all the variables and constants involved in a monomial term. On the other hand, polynomials have the highest degree. For example, a quadratic function 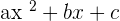 has the highest degree 2.
has the highest degree 2.
Find the best Maths tutor on Superprof.
Like Monomials
Now, we will see what are like or similar monomials. Two monomials having the same literal part are termed as like terms or similar monomials. We can apply the operations of addition and subtraction on like monomial terms to get a monomial.
For example, the monomial terms  and
and 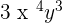 are like or similar monomials because they have the same literal parts, despite having different coefficients. Similarly, the monomials
are like or similar monomials because they have the same literal parts, despite having different coefficients. Similarly, the monomials  and
and  are also like terms because of the common literal part
are also like terms because of the common literal part  .
.
Now, we will see how to apply arithmetic operations such as addition, subtraction, multiplication and division on the monomials.
Addition
We add two or more monomials which have the same literal part by summing the coefficients together, while not changing the variables and their degrees. The examples of this operation are given below:
1. Add 
We will add these monomial terms like we add numbers and fractions like this:
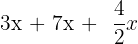
The L.C.M of these three numbers is equal to 2.

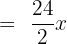

Hence, you can see that when the same monomials are added together, the result is also a monomial.
2. Add 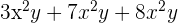
Simply add the coefficients of these monomial terms to get another monomial. The result will be 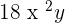 .
.
Subtraction
The subtraction of two or more monomials is carried out by subtracting the coefficients like numbers, while keeping the literal part the same. Consider the following examples:
1. Subtract 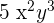 from
from 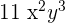
Subtract 11 from 5 and keep the literal part of the expression the same. The result will be 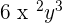 .
.
2. Solve 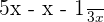
When we take L.C.M. of the three terms, we will get 3.
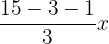
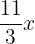
Do not confuse the rule of the monomial here which says that a monomial cannot have fractional or negative exponents. In the above example, we do not have fractional exponent, rather we have a fractional coefficient. Hence, the above answer is a monomial term.
Thus, we can conclude from the above two examples that by subtracting 2 or more monomials that have the same literal part, we get another monomial. Remember that adding and subtracting monomials will result in another monomial term if and only if the terms involved are like terms. Otherwise, we may get polynomial functions such as binomial or trinomials.
Multiplication
Now we will see how to multiply the monomials.
Multiplication of the monomials has two steps:
- The coefficients are multiplied together
- The exponents are multiplied together by adding up their powers
Multiplication and division of monomials do not follow the rule of addition and subtraction which say that to get a monomial, the monomials involved should have the same literal parts. Even if the monomials do not have the same literal part, we can get a monomial term as a result of their multiplication or division
Let us explain this concept through the following examples.
1. Multiply  by
by 
To simplify, first, 5 will be multiplied by 7 to get 35. Now, we will multiply the literal parts of the monomials together by adding their exponents.
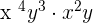
=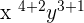
= 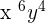
The whole expression will be 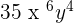 .
.
2. Solve 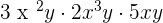
To simplify, first multiply the coefficients 3 , 2 and 5 together. Multiplying them will give us an answer 30. Now, we will see how to simplify the literal parts:
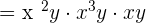
= 
= 
We will write the final answer by multiplying the resulting constant term and the variables together. Hence, 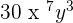 is the answer to the above question.
is the answer to the above question.
Hence, through the above examples, we can conclude that multiplying the monomials will yield another monomial, regardless of the fact that their literal parts are different.
Division
Dividing monomials is quite simple, unlike dividing polynomials which are divided by complex polynomial long division method.
- Dividing the coefficients of the monomial terms
- Dividing the like variables by subtracting their exponents in the final answer
Consider the following examples:
1. Divide 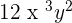 by
by  .
.
Let us rewrite this questions as 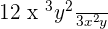 .
.
12 divided by 3 will give us 4. The variable  and
and  in the numerator will be divided by the variables
in the numerator will be divided by the variables  and
and  in the denominator. The exponents in the numerator and denominator will be simplified like this:
in the denominator. The exponents in the numerator and denominator will be simplified like this:
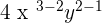
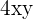
The answer 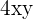 is also a monomial.
is also a monomial.
Keep in mind that the division of two monomials does not always yield a monomial term. Consider the following example:
2. 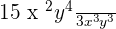
When we divide 15 by 3, we will get the answer 3. Let us see what will be the literal part of the answer.
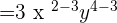
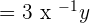
The above answer is not a monomial term because if we recall the rules of the monomial, we will get to know that any algebraic expression with a negative or fractional exponent is not a monomial term. Hence,  is not monomial.
is not monomial.
Summarise with AI: