Chapters
- Exercise 1
- Exercise 2
- Exercise 3
- Exercise 4
- Exercise 5
- Exercise 6
- Exercise 7
- Exercise 8
- Exercise 9
- Exercise 10
- Solution of exercise 1
- Solution of exercise 2
- Solution of exercise 3
- Solution of exercise 4
- Solution of exercise 5
- Solution of exercise 6
- Solution of exercise 7
- Solution of exercise 8
- Solution of exercise 9
- Solution of exercise 10

Exercise 1
State whether the following algebraic expressions are polynomials or not. In the affirmative case, indicate what its degree and independent term are.
1 x4 − 3x5 + 2x² + 5
2 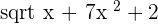
3 1 − x4
4 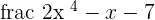
5 x³ + x5 + x²
6 x − 2x−3 + 8
7 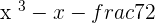
Exercise 2
Write:
1 An ordered polynomial without a constant term.
2 A complete polynomial but not orderly.
3A complete polynomial without an independent term.
4 A polynomial of degree 4, complete with odd coefficients.
Exercise 3
Given the polynomials:
P(x) = 4x² − 1
Q(x) = x³ − 3x² + 6x − 2
R(x) = 6x² + x + 1
S(x) = 1/2x² + 4
T(x) = 3/2x² + 5
U(x) = x² + 2
Calculate:
1P(x) + Q (x) =
2P(x) − U (x) =
3P(x) + R (x) =
42P(x) − R (x) =
5S(x) + T(x) + U(x) =
6S(x) − T(x) + U(x) =
Exercise 4
Given the polynomials:
P(x) = x4 − 2x² − 6x − 1
Q(x) = x³ − 6x² + 4
R(x) = 2x4 − 2x − 2
Calculate:
P(x) + Q(x) − R(x) =
P(x) + 2 Q(x) − R(x) =
Q(x) + R(x) − P(x)=
Exercise 5
Multiply:
1(x4 − 2x² + 2) · (x² − 2x + 3) =
2 (3x² − 5x) · (2x³ + 4x² − x + 2) =
3 (2x² − 5x + 6) · (3x4 − 5x³ − 6x² + 4x − 3) =
Exercise 6
Divide:
1(x4 − 2x³ − 11x²+ 30x − 20) : (x² + 3x − 2)
2(x 6 + 5x4 + 3x² − 2x) : (x² − x + 3)
3 P(x) = x5 + 2x³ − x − 8 Q(x) = x² − 2x + 1
Exercise 7
Divide using Ruffini's rule:
1 (x³ + 2x + 70) : (x + 4)
2(x5 − 32) : (x − 2)
3 (x4 − 3x² + 2 ) : (x −3)
Exercise 8
Find the remainder of the following divisions:
1(x5 − 2x² − 3) : (x −1)
2(2x4 − 2x³ + 3x² + 5x + 10) : (x + 2)
3 ( x4 − 3x² + 2) : (x − 3)
Exercise 9
Indicate which of these divisions are exact:
1(x³ − 5x −1) : (x − 3)
2(x6 − 1) : (x + 1)
3(x4 − 2x³ + x² + x − 1) : (x − 1)
4(x10 − 1024) : (x + 2)
Exercise 10
Verify the following statements:
1(x³ − 5x −1) has of factor (x − 3)
2(x6 − 1) has of factor (x + 1)
3(x4 − 2x³ + x² + x − 1) has of factor (x − 1 )
4(x10 − 1024) has of factor (x + 2)
Find the best Maths tutors on Superprof.
Solution of exercise 1
1State whether the following algebraic expressions are polynomials or not. In the affirmative case, indicate what its degree and independent term are.
1x4 − 3x5 + 2x² + 5
Degree: 5, independent term: 5.
2 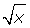
It is not a polynomial because the literal part of the first monomial is within a root.
31 − x4
Degree: 4, independent term: 1.
4 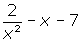
It is not a polynomial because the exponent of the first monomial is not a natural number.
5x³ + x5 + x²
Degree: 5, independent term: 0.
6x − 2 x−3 + 8
It is not a polynomial because the exponent of the 2nd monomial is not a natural number.
7 
Degree: 5, independent term: −7/2.
Solution of exercise 2
Write:
1 An ordered polynomial without a independent term.
3x4 − 2x
2 A complete polynomial but not orderly.
3x − x² + 5 − 2x³
3A complete polynomial without an independent term.
Impossible
4 A polynomial of degree 4, complete with odd coefficients.
x4 − x³ − x² + 3x + 5
Solution of exercise 3
Given the polynomials:
P(x) = 4x² − 1
Q(x) = x³ − 3x² + 6x − 2
R(x) = 6x² + x + 1
S(x) = 1/2x² + 4
T(x) = 3/2x² + 5
U(x) = x² + 2
Calculate:
1P(x) + Q (x) =
= (4x² − 1) + (x³ − 3x² + 6x − 2) =
= x³ − 3x² + 4x² + 6x − 2 − 1 =
= x³ + x² + 6x − 3
2P(x) − U (x) =
= (4x² − 1) − (x² + 2) =
= 4x² − 1 − x² − 2 =
= 3x² − 3
3P(x) + R (x) =
= (4x² − 1) + (6x² + x + 1) =
= 4x² + 6x² + x − 1 + 1 =
= 10x² + x
42P(x) − R (x) =
= 2 · (4x² − 1) − (6x² + x + 1) =
= 8x² − 2 − 6x² − x − 1 =
= 2x² − x − 3
5S(x) + T(x) + U(x) =
= (1/2 x² + 4 ) + (3/2 x² + 5 ) + (x² + 2) =
= 1/2 x² + 3/2 x²+ x² + 4 + 5 + 2 =
= 3x² + 11
6S(x) − T(x) + U(x) =
= (1/2 x² + 4) − (3/2 x² + 5) + (x² + 2) =
= 1/2 x² + 4 − 3/2 x² − 5 + x² + 2 =
= 1
Solution of exercise 4
Given the polynomials:
P(x) = x4 − 2x² − 6x − 1
Q(x) = x³ − 6x² + 4
R(x) = 2x4 − 2 x − 2
Calculate:
P(x) + Q(x) − R(x) =
= (x4 − 2x² − 6x − 1) + (x³ − 6x² + 4) − ( 2x4 − 2 x − 2) =
= x4 − 2x² − 6x − 1 + x³ − 6x² + 4 − 2x4 + 2x + 2 =
= x4 − 2x4 + x³ − 2x² − 6x² − 6x + 2x − 1 + 4 + 2 =
= −x4 + x³ − 8x² − 4x + 5
P(x) + 2 Q(x) − R(x) =
= (x4 − 2x² − 6x − 1) + 2 · (x³ − 6x² + 4) − (2x4 − 2x − 2) =
= x4 − 2x² − 6x − 1 + 2x³ − 12x² + 8 − 2x4 + 2x + 2 =
= x4 − 2x4 + 2x³ − 2x² − 12x² − 6x + 2x − 1 + 8 + 2 =
= −x4 + 2x³− 14x² − 4x + 9
Q(x) + R(x) − P(x)=
= (x³ − 6x² + 4) + (2x4 − 2x − 2) − (x4 − 2x² − 6x − 1) =
= x³ − 6x² + 4 + 2x4 −2x − 2 − x4 + 2x² + 6x + 1=
= 2x4 − x4 + x³ − 6x² + 2x² −2x + 6x + 4 − 2 + 1=
= x4 + x³ − 4x² + 4x + 3
Solution of exercise 5
Multiply:
1(x4 − 2x² + 2) · (x² − 2x + 3) =
= x 6 − 2x5 + 3x4 − 2x4 + 4x³ − 6x² + 2x² − 4x + 6=
= x 6 − 2x5 − 2x4 + 3x4 + 4x³ + 2x² − 6x² − 4x + 6 =
= x 6 −2x5 + x4 + 4x³− 4x² − 4x + 6
2 (3x² − 5x) · (2x³ + 4x² − x + 2) =
= 6x5 + 12x4 − 3x³ + 6x² − 10x4 − 20x³ + 5x² − 10x =
= 6x5 + 12x4 − 10x4 − 3x³ − 20x³ + 6x² + 5x² − 10x =
= 6x5 + 2x4 − 23x³ + 11x² − 10x
3 (2x² − 5x + 6) · (3x4 − 5 x³ − 6 x² + 4x − 3) =
= 6x6 − 10x5 − 12x4 + 8x³ − 6x² −
− 15x5 + 25x4 + 30x³ − 20x² + 15x +
+18x4 − 30x³ − 36x² + 24x − 18 =
= 6x6 − 10x5 − 15x5 − 12x4 + 25x4 + 18x4 +
+8x³ − 30x³ + 30x³ − 6x²− 20x² − 36x² + 15x + 24x − 18 =
= 6x6 − 25x5 + 31x4 + 8x³ − 62x² + 39x − 18
Solution of exercise 6
Divide:
1 (x4 − 2x³ − 11x² + 30x − 20) : (x² + 3x − 2)

2(x 6+ 5x4 + 3x² − 2x) : (x² − x + 3)
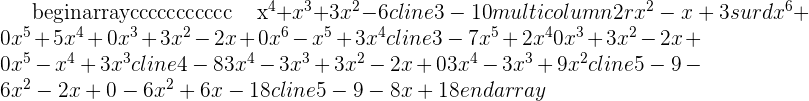
3 P(x) = x5 + 2x³ − x − 8 Q(x) = x² − 2x + 1

Solution of exercise 7
Divide using Ruffini's rule:
1 (x³ + 2x +70) : (x + 4)


2(x5 − 32) : (x − 2)
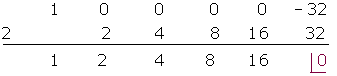
C(x) = x4 + 2x³ + 4x² + 8x + 16 R = 0
3 (x4 −3x² +2) : (x −3)

C(x) = x³ + 3x² + 6x +18 R = 56
Solution of exercise 8
Find the remainder of the following divisions:
1(x5 − 2x² − 3) : (x −1)
Apply the remainder theorem:
R(1) = 15 − 2 · 1² − 3 = −4
2(2x4 − 2x³ + 3x² + 5x +10) : (x + 2)
Apply the remainder theorem:
R(−2) = 2 · (−2)4 − 2 · (−2)³ + 3 · (−2)² + 5 · (−2) +10 =
= 32 + 16 + 12 − 10 + 10 = 60
3 (x4 − 3x² +2) : ( x − 3)
Apply the remainder theorem:
P(3) = 34 − 3 · 3² + 2 = 81 − 27 + 2 = 56
Solution of exercise 9
Indicate which of these divisions are exact:
1(x³ − 5x −1) : (x − 3)
Apply the remainder theorem:
P(3) = 3³ − 5 · 3 − 1 = 27 − 15 − 1 ≠ 0
It is not exact.
2(x6 − 1) : (x + 1)
Apply the remainder theorem:
P(−1)= (−1)6 − 1 = 0
Exact.
3(x4 − 2x³ + x² + x − 1) : (x − 1)
Apply the remainder theorem:
P(1) = 14 − 2 · 1³ + 1 ² + 1 − 1 = 1 − 2 +1 +1 − 1 = 0
Exact.
4(x10 − 1024) : (x + 2)
Apply the remainder theorem:
P(−2) = (−2)10 − 1024 = 1024 − 1024 = 0
Exact.
Solution of exercise 10
Verify the following statements:
1(x³ − 5x −1) has of factor (x − 3)
Apply the factor theorem:
(x³ − 5x −1) is divisible by (x − 3) if and only if P(x = 3) = 0.
P(3) = 3³ − 5 · 3 − 1 = 27 − 15 − 1 ≠ 0
(x − 3) is not a factor.
2(x6 − 1) has of factor (x + 1)
Apply the factor theorem:
(x6 − 1) is divisible by (x + 1) if and only if P(x = − 1) = 0.
P(−1) = (−1)6 − 1 = 0
(x + 1) is a factor.
3(x4 − 2x³ + x² + x − 1) has of factor (x − 1)
Apply the factor theorem:
(x4 − 2x³ + x² + x − 1) is divisible by (x − 1) if and only if P(x = 1) = 0.
P(1) = 14 − 2 · 1³ + 1 ² + 1 − 1 = 1 − 2 +1 +1 − 1 = 0
(x − 1) is a factor.
4(x10 − 1024) has of factor (x + 2)
Apply the factor theorem:
(x10 − 1024) is divisible by (x + 2) if and only if P(x = −2) = 0.
P(−2) = (−2)10 − 1024 = 1024 − 1024 = 0
(x + 2) is a factor.
Summarise with AI:













