Chapters

What is the Binomial Theorem?
Let's imagine you came across an equation 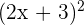 , the first thing that will come in your mind will be to open the equation by using
, the first thing that will come in your mind will be to open the equation by using  formula. What if you came across
formula. What if you came across 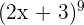 ? It might seem impossible to open this equation but there is nothing such as impossible in maths!
? It might seem impossible to open this equation but there is nothing such as impossible in maths!
To expand high power equations, we use Binomial Theorem. Binomial is a polynomial with two terms. Let's take the above example once again, how many terms are there in 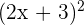 ? If your answer is 2 then you are correct! The first term is
? If your answer is 2 then you are correct! The first term is  and the second term is
and the second term is  . You can expand this equation with polynomial multiplication. This is how you will solve using polynomial multiplication it:
. You can expand this equation with polynomial multiplication. This is how you will solve using polynomial multiplication it:

However, as you move forward, you will encounter equations with high power. To expand those equations, without making any errors, we use the binomial theorem.
In algebra, Binomial Theorem is a method through which we can expand high power equations. The binomial theorem has only two limitations.
- The power should be positive,
- The power should be in whole numbers.
If you find an equation having a negative power or the power is in fraction form then you can't apply the binomial theorem. To solve those equations, we use a different technique which we will discuss later. The expression of the binomial theorem is:

where:
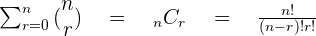
 is the exponent of the equation
is the exponent of the equation
 is the number of terms
is the number of terms
Factorial Notation
Did you notice an exclamation mark after n and r? In mathematical language, we call it Factorial Notation. This notation means to multiply all whole numbers (starting from 1) to nth value. Let's create an example, your teacher asked you to find the factorial of number 6. You will write it like this "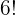 ". This is how you will expand:
". This is how you will expand:

Pretty simple, right? To expand high power equations, you need to understand factorial notation. There are many methods to expand the high power equation. The oldest way to find this value is through Pascal's Triangle.
Pascal's Triangle
This method was invented by a famous French mathematician. His name is Blaise Pascal (1623 - 1662) and he made a triangular array in which numbers were added in adjacent elements in preceding rows. Here is a small example of Pascal's Triangle.

The triangle doesn't end here. As a matter of fact, it keeps going on. In other words, the pascal's triangle goes to infinity.
Let's break the triangle into rows. We will call the first row as 0th Row. The second row will be our 1st Row. Keep naming the row, in the end, it will be like this.
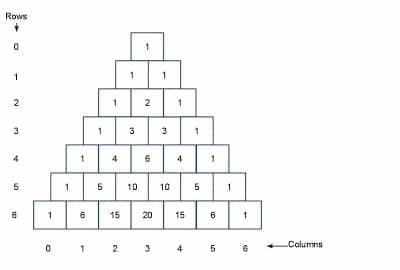
Suppose, you were assigned to expand 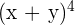 . First of all, you need to select the row according to your power. In
. First of all, you need to select the row according to your power. In 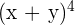 , the exponent is
, the exponent is  , therefore we will pick the 4th row.
, therefore we will pick the 4th row.
Now take all the values from the 4th row and use "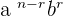 " formula to enter all the x's and y's values like this:
" formula to enter all the x's and y's values like this:

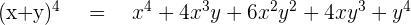
Don't forget that the "n" represents number of terms. Since the power is up to 4 therefore, we can expand it till 5 terms (since the row starts from 0). However, "r" represents the row like in this question we were talking about 4th row so r=4.
Check for maths tuition here.
Combination Formula
If your factorial notation concept is clear then understanding combination formula will be a piece of cake. The formula of combination is below:

Don't worry, it might look scary but in reality, it is a very simple formula. To understand this formula, you should remember about "n" and "r". For example, you need to find the value of 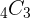 , you need to use the above formula and replace all the n's and r's with the given values.
, you need to use the above formula and replace all the n's and r's with the given values.
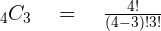
Now, use the knowledge about factorial and apply here, it should look like this:
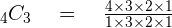
Since it just transformed into simple division, start dividing! Your final answer should be this:
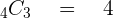
Now it doesn't look scary, right? If you put all the values in the right place then you should have no trouble in finding the value!
However, there is another method to find combination values. You can use a scientific calculator to find the value. Although we don't recommend you to use a calculator to find the value of the algebraic term's power is very high then to save time, you can use a calculator.
Take out your scientific calculator and search for a button label as "C" or "nCr".
Let's take the above example of 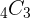 again. To find the value of
again. To find the value of 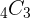 , you need to press 4 first. Then you need to press the "C" button. Last but not least, to insert the value of r, press 3 and then press "=" or "sol" button. It will provide you the value of
, you need to press 4 first. Then you need to press the "C" button. Last but not least, to insert the value of r, press 3 and then press "=" or "sol" button. It will provide you the value of 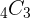 which is "4".
which is "4".
In case if your calculator has the "nCr" button then there is a slightly different method. Press that button and then put the value of n and r and then press the "=" or "sol" button to get your answer.
For example, you need to expand  using the combination formula, this is how you will expand the equation:
using the combination formula, this is how you will expand the equation:

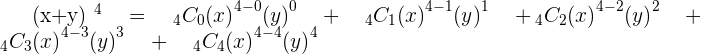
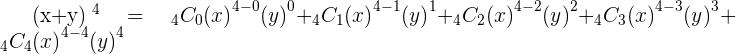
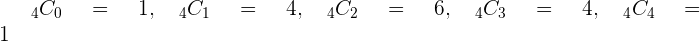

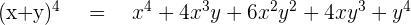
Let's create another example but this time we used minus sign between both variables.
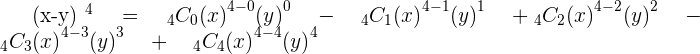
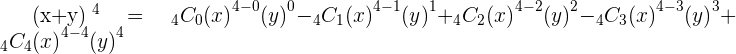
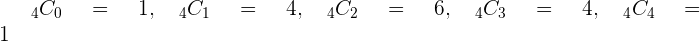
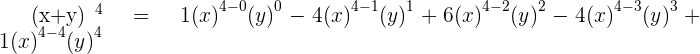

Further Examples of Combination.
Example No.1: 
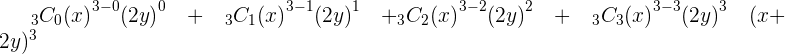
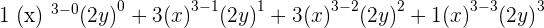
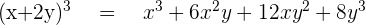
Example No.2: 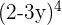



Example No.3: 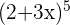
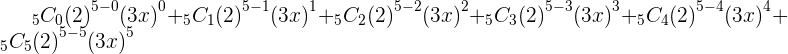
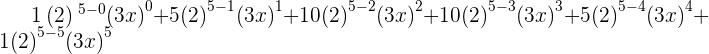
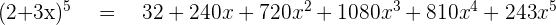
Example No.4: 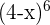
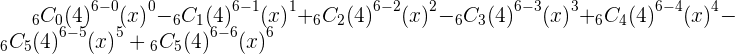
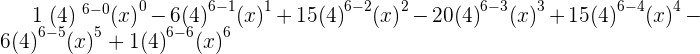
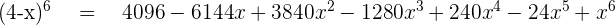
Example No.5: 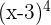
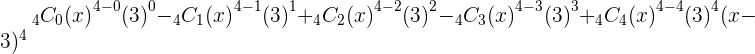
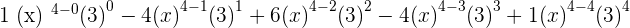
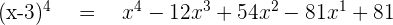
Finding The Specific Term
Sometimes, you need a specific term. Let's say that we want the 2nd term of 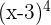 . To find the 2nd term, we don't need to expand the whole equation instead I will expand only the 2nd term of the equation. Remember, binomial starts at 0. This means you need to start at 0 and then find the term. We got a small trick for you. Whatever the term you are given, just subtract one from the term and that is your nth value.
. To find the 2nd term, we don't need to expand the whole equation instead I will expand only the 2nd term of the equation. Remember, binomial starts at 0. This means you need to start at 0 and then find the term. We got a small trick for you. Whatever the term you are given, just subtract one from the term and that is your nth value.
Let's take the above example again. To find the 2nd term of 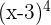 , you need to subtract 1 from 2. The answer will be 1 so that is your nth value now put it in the formula.
, you need to subtract 1 from 2. The answer will be 1 so that is your nth value now put it in the formula.
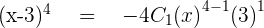

This means that the 2nd term of 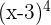 is
is  . Please do note the minus sign, on even nth value, the sign will be positive and on odd the sign will be negative.
. Please do note the minus sign, on even nth value, the sign will be positive and on odd the sign will be negative.
Further Examples of Finding The Specific Term
1. Find the fifth term of the development 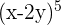 .
.
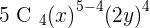

2. Find the fourth term of the development  .
.
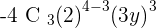

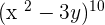
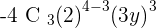
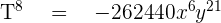
4. Find the fifth term of the development 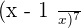 .
.
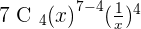
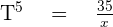
5. Find the independent term of development 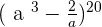 .
.
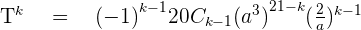
In case if you have any questions in your mind, let us know in the comments.
Summarise with AI:













