Chapters

Meaning of Remainder, Divisor, and Quotient
From the start, we have been solving problems related to dividing however many students don't have the proper concept of dividing. A student needs to know all the terms. Let's create an example, you are dividing 5 by 3. When you divide 5 by 3 then you will get 2 at the bottom of the division. That 2 is known as the remainder. The word remainder means the leftover part of something. Since we can't divide 2 by 3, therefore, we leave it as a remainder.
A dividend is a number or variable which will be divided by divisor. A divisor is a number or variable which divides the dividend. Last but not least, the quotient is the result after dividing the dividend by divisor. In the above case, 5 is the dividend however 3 is the divisor. Let's arrange them in a mannerly way.
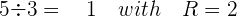
Where,
5 is the dividend,
3 is the divisor,
1 is the quotient,
and 2 is the remainder.
The above can be written in this form as well:
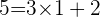
Dividing Polynomials
The remainder of the division of a polynomial P(x) and a polynomial of the form 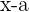 is the numerical value of this polynomial for the value:
is the numerical value of this polynomial for the value:  .
.
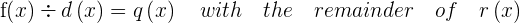
We can rewrite in this way as well:

Long Division
Long division is one of the easiest method to find the remainder and quotient. It is almost same as the normal division that you encounter. Here is an example of long division.
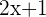


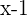
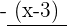
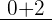
Here we divided  with
with  and the quotient is
and the quotient is  and remainder is
and remainder is  . Do make sure that you check the signs. When you are dividing, you put a minus sign, so be careful when you are choosing your signs. This is a very common mistake that many people make. If we talk about "
. Do make sure that you check the signs. When you are dividing, you put a minus sign, so be careful when you are choosing your signs. This is a very common mistake that many people make. If we talk about " " style then it will be written as:
" style then it will be written as:

Here is another example of a long division.
Example: 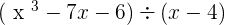
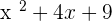


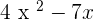


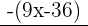
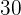
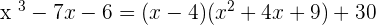
Example: 
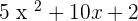
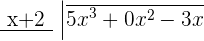
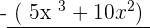

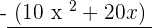
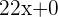
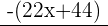


Synthetic Division
Synthetic division is different than long division. Many people prefer synthetic division because it is short and more accurate than long division. For example, you got a question 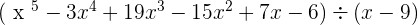 , this will take you forever to solve it and not to forget if you made any error then it will be difficult to locate and verify however if you make an error in synthetic division, you will find it easily.
, this will take you forever to solve it and not to forget if you made any error then it will be difficult to locate and verify however if you make an error in synthetic division, you will find it easily.
How To Do Synthetic Division
It might look difficult at the start but if you practice it a lot then it will become a piece of cake for you. Here are the steps to do synthetic division.
Q. 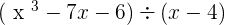 . Solve it using synthetic division method.
. Solve it using synthetic division method.
STEP 1:
Write all the coefficients of the variables and arrange them in ascending order (with respect to their exponent). Moreover, do include the signs as well.
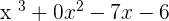

STEP 2:
Make a synthetic table(like shown below) and add the divisor on the left of the table. To find the divisor, you need to equate the expression by making it equal to zero.

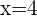

Step 3:
The first term will be written down as it is and then you need to multiply it to the divisor. The resulting number will be shifted in the second term and then add or either subtract it from the second term (depends on the second term's sign).

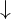





Step 4:
Now keep multiplying the carry-down value of the previous term with the divisor and then add or subtract from the term.



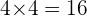







The last term of your result is the remainder this means that the rest is the quotient. This can be written as below:
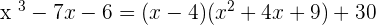
Check out affordable Maths tuition on Superprof.
How To Find Remainder Without Synthetic Division
Sometimes, your concern is with the remainder only. To find the remainder, you don't need to do the whole synthetic division instead there is a way through which you can easily find the remainder in just 2 steps. Below are the steps to find the remainder without synthetic division.
Step 1:
You need to create an equation of divisor by making it equal to zero like shown below:

Now find the value of x.
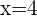
Step 2:
Put the value of x in the polynomial expression and the answer will be your remainder.
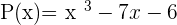
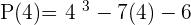
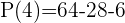
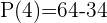

Example
Calculate the remainder of the division P(x):Q(x)
P(x)= x4 − 3x² + 2 Q(x) = x − 3
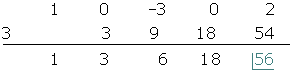
P(3) = 34 − 3 · 3² + 2 = 81 − 27 + 2 = 56
Summarise with AI:













