
What Do You Mean By Polynomial?
Till now you might have encountered quadratic equations (or expressions) and straight-line equations. However, it is just the beginning of algebra. For the straight-line equation, you might have noticed that you got only one number as your answer. In the quadratic equation or expression, you got two different answers and both will give the same answer when you plug in the value in the equation or expression. Does this mean that the power of the variable is limited to two? Of course no! It can be 3, 4, 5, 6, and it continues to go on.
There is no limitation on the power of the variable. Although the higher the power, the difficult it will be to solve as well as there will be many answers to just one equation or expression. If the power of the variable (in an equation) is greater than 2 then we will call it a polynomial equation. Poly means many. Let's make it simple, poly means more than one. So does this mean that the quadratic equation is a polynomial equation? Let's find it out.
First of all, we will create a quadratic expression and do the analysis. Here is your quadratic expression:
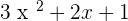
Check the exponent of x in the above expression. The first term has power "2" and the second term has power "1". The third term has power "0". We can call it a polynomial equation since the first term exponent is "2", on that basis we can declare that all quadratic equations or expressions are also polynomial. Let's take another example.

Take a few seconds to analyze the above expression and think is this a polynomial expression? If your answer is yes then good job! We can call it a polynomial expression, why? Because it satisfies all the conditions. If you notice, that is a straight-line expression. Here is another example for you but this one is tricky.

This time the exponent is negative so can we declare it as a polynomial expression? No, because of the negative exponential. Remember, the exponent should be a positive integer. Here is another case, check it carefully and think is it either a polynomial expression or not?
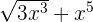
If your answer is no then you are correct! Why? Because the exponent should be an integer and the above equation is in radical form. However, polynomial equation or expression isn't all about exponents, coefficient also plays an important role. The coefficient should be a real number otherwise it won't be a polynomial equation or expression.
Here is a question for you to test whether you understand perfectly or not.

Look at the expression carefully and then keep all the conditions in your mind before you make your prediction. If your answer is yes then congratulations! Now you know how to differentiate between polynomial expression. The reason why it is a polynomial expression is that it follows all the rules. The exponent is an integer and positive and if we check the coefficient, it is a real number, therefore, we can declare it a polynomial expression. In case if you though that the root is on the "x" as well then no you are wrong. Check it again, the root ends before the x.
Find good maths tutors near me here.
Degree of Polynomial
In the world of Algebra, "Degree" means "Order". In other words, the degree of a polynomial is the highest exponent in the polynomial. For example, your teacher asked you to find the degree of the following expression:
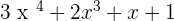
The degree will be "4" because if you look at the expression, the highest exponent is "4" which is present in the first term. It isn't necessary that the degree will be the first term. The keyword is the "highest exponent". So, if you spot the highest exponent that means you just spot the degree of the equation.
How To Add Polynomials
P(x) = 
Q(x) = 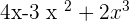
Step 1
If they are not of the same degree, order the polynomials.
Q(x) = 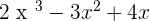
P(x) + Q(x) = 
Step 2
Group the monomials of the same degree.
P(x) + Q(x) = 
Step 3
Add the similar monomials.
P(x) + Q(x) = 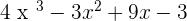
You can add more than 2 polynomials. For example:
P(x) = 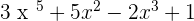
Q(x) = 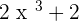
R(x) = 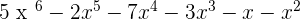
Step 1: Ordering the polynomials
P(x) = 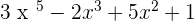
R(x) = 
P(x) + Q(x) + R(x) = 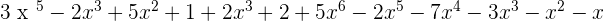
Step 2: Arrange them according to their degrees
P(x) + Q(x) + R(x) = 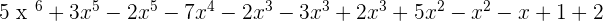
Step 3: Add all the degrees
P(x) + Q(x) + R(x) = 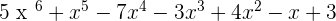
Q.1 Add the following polynomials.
A(y) = 
B(y) = 
C(x) = 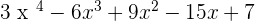
Step 1:
*We don't need to order since the degrees are already in order.
A(y) + B(y) + C(x) = 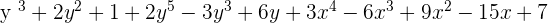
Step 2:
A(y) + B(y) + C(x) = 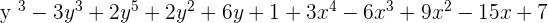
Step 3:
A(y) + B(y) + C(x) = 
A(y) + B(y) + C(x) = 
Q.2 Add the following polynomials.
F(x) = 
G(x) = 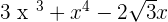
Step 1:
F(x) = 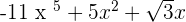
G(x) = 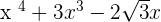
F(x) + G(x) = 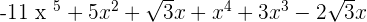
Step 2:
F(x) + G(x) = 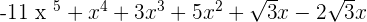
Step 3:
F(x) + G(x) = 
Q.3 Add the following polynomials.
W(t) = 
X(t) = 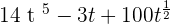
The answer will be not possible since the exponent isn't an integer.













