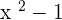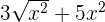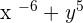What is Polynomial
The word poly means more than 1 or in easy words "many". The word nominal means mathematical expression. If we combine both definitions then polynomial means an algebraic expression or equation which contains more than one term. Almost all equations in algebra are polynomial equations. Whether it is a quadratic equation or straight-line equation, you can call it a polynomial equation.
However, polynomial equations have some limitations. These limitations are discussed in the previous post but let's just revise it here. There are two conditions for a polynomial expression or equation.
- The exponent of the variable should be a positive integer
- The coefficient should be a real number
- There should be more than one mathematical expression
This means that if any condition is void then you can't call it a polynomial equation or expression. Let's create some expressions and you try to think either the expressions are a polynomial equation or not?
The first three and the sixth option are polynomial expressions and the rest are not. If you look carefully, the first two expressions satisfy all the conditions and therefore we can declare it a polynomial equation. However, in the third expression, there is a square root on a variable with a square. If we simplify it then it will be 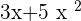 which means that it is a polynomial expression.
which means that it is a polynomial expression.
In the case of the fourth expression, you can see a negative sign with the exponent. The exponent is an integer, there is no doubt but remember that the integer should be a positive number otherwise it won't be a polynomial expression. In the fifth one, the same reason but a different approach. The variable is in fraction form. It might look like a polynomial but don't let the question deceive you. If you reciprocate it, the exponent will be converted into a negative term and hence negative exponent voids the condition of the polynomial.
The sixth one is also a polynomial. The reason is that it fulfills all the conditions. The name of this polynomial is monomial. Last but not least, the seventh expression has a problem. The variable and the exponent satisfy their conditions but the coefficient has a problem. The coefficient of this expression is a negative number inside a square root. In simple words, it is an imaginary number (a number which doesn't exist in real life). In conclusion, it is not a polynomial expression.
What is the difference between an expression and an equation?
To easily understand, let's examine the below equation and expression:


The first one is the algebraic expression and the next one is the algebraic equation. How can we differentiate between an equation and an expression? The word equation means to equate to something. If you look at the equation, the left-hand side is equal to the right-hand side in this case, it is equal to zero. It is not necessary that the left-hand side is always zero, it can be any number or variable. The keyword is the "is equal to" symbol. If you see this symbol that means it is an equation.
The word expression means something which is expressed. It doesn't mean to express it in words but it just an expression telling you something. In the first option, you see an expression that tells you the variables, coefficients, and constants. In the mathematical world, we deal with the equations mostly because you can't do anything to an expression (unless you have been asked to factorize it).
Find the best Maths tutors on Superprof.
Formulas
There are many formulas for different polynomial expressions or equations. Before we start with the formulas, you should know the categories of polynomials. There are three types of polynomial, below are the types of polynomials.
- Monomials
- Binomials
- Trinomials
Monomials


This means if the exponent and the variables are the same then you can take out as common and add or subtract their coefficients.

If the bases (which is the variable in this case) are the same and there is a multiplication sign then it means that the exponent will be the sum of both and the coefficient will be the product of both.
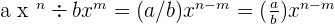
If the bases (which is the variable in this case) are the same and there is a division or ratio sign then it means that the exponent will be the difference of the second term from the first term and the coefficient will also be divided in that order.

If there is an exponent on a term that also has an exponent then the resulting exponent will be the product of both exponents.
Binomials
We can split the term binomial into two which are bi and nomial. The word bi means 2 and nomial mean mathematical expression. In other words, if there are two mathematical terms then that expression or equation will be binomial. Below are the formulas for binomials.


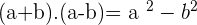
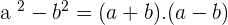

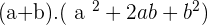
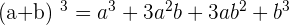
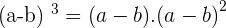
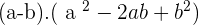

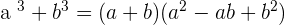

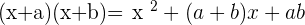
Trinomials
Like binomial, we can also break trinomial into two terms which are tri and nomial. Tri means "3" and nomial means mathematical term. In conclusion, we will declare an equation or expression as trinomial if the equation or expression contains "3" terms. Below are all the formulas for trinomials equation or expression.
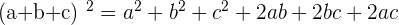
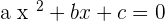
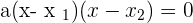 *also known as quadratic equation
*also known as quadratic equation
Summarise with AI: