Chapters

How Does a Polynomial Look Like?
Maths is divided into three categories and one of them is "Algebra". If you made it till here that means you have a great understanding of straight-line equations as well as quadratic equations. However, the algebraic expression doesn't end here. In other words, you will also find higher power equations.
Under the heading of straight-line equations, you learned that the value of the variable is fixed. Straight-line equations are straight forward and easy to solve however, quadratic equations might be a little complex. We get two different answers of a variable in the quadratic equation and both of them satisfy the equation. If we draw the graph of both equations, the straight-line equation will have a straight line however you will see a curve in case of a quadratic equation. The curve will be "U-shape" and you can even say that the curve is symmetrical.
What about equations or expressions that have exponents greater than 2? We call them the polynomial. The word polynomial can be broken into two, which are poly and nomial. The meaning of poly is 2 or more than 2 and the meaning of nomial is a mathematical term. Therefore, we can say polynomial means an equation or expression which consists of many terms. In simple words, a polynomial equation is an equation that consists of 2 or more than 2 algebraic expressions which will have different exponents of the same variables. Below is an example of a polynomial expression:
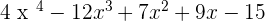
where,
x is the variable,
 , where n is the exponent of the variable,
, where n is the exponent of the variable,
+ and - are the mathematical operations,
and 15 is the constant.
How To Identify Either the Equation/Expression is Polynomial or Not?
You can't declare an algebraic expression with multiple terms as polynomial every time. As a matter of fact, there are a few conditions that you need to keep in mind. First of all, the exponent should be a positive integer. The second condition is that the coefficient should be a real number. Let's create different cases and then we will do an analysis that either the expression is polynomial or not.
Case Number 1:
Below is the expression, look it carefully and then remember the conditions of the polynomial and then think either it is a polynomial or not?

If your answer is yes then you are correct! Why? First of all, check the exponents. They are all positive integers, therefore, this gives a green light. Now check the coefficient, they are real numbers. Therefore it is a polynomial expression.
Case Number 2:
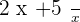
Take a few seconds and think either the above expression is a polynomial expression or not? The answer is no, first of all simply the expression. After simplification, the expression will look like this.
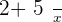
The second term has a variable in fraction form. This means the exponent of the variable will be  and it isn't a positive integer. Remember, the exponent should be a positive integer.
and it isn't a positive integer. Remember, the exponent should be a positive integer.
Case Number 3:

If your answer is no then you are correct! If you look carefully, the variable is trapped in a cube root. This means the exponent is 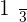 . Fractions are not integers, therefore, the above expression isn't a polynomial expression.
. Fractions are not integers, therefore, the above expression isn't a polynomial expression.
Case Number 4:
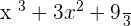
Case number 4 is a bit different than the case number 1. The answer is yes because it satisfies all the conditions, why? Simplify the above expression and then you might get your answer.

Now it is simplified and you can easily understand. All the exponents are positive integers. Furthermore, the coefficients are real numbers. In conclusion, the above expression is a polynomial expression.
Degree of Polynomials
Another word of degree is "Order". The degree is the highest exponent in the polynomial expression or equation. For example, your teacher asked you to find the degree of  , the answer will be "
, the answer will be " " because, in that expression, the highest power is
" because, in that expression, the highest power is  , therefore, the degree of that expression is "
, therefore, the degree of that expression is " ".
".
That expression was pretty simple however there are some steps through which you can find out the degree of any polynomial expression or expression. Below are the steps:
EXAMPLE: 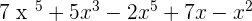
Step 1: Arrange the expression/equation in ascending order

Step 2: Perform the mathematical operation if possible
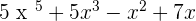
Step 3: Ignore all the coefficients
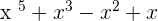
Step 4: The largest exponent is the degree of the expression
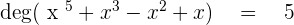
Find the best Maths tutor on Superprof.
How To Multiply Polynomials
Multiplication of a constant by a polynomial
If the polynomial is multiplied by a constant then the coefficients are the product of the coefficients of the polynomial and the number.
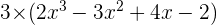

Multiplication of a Monomial by a Polynomial
The monomial is multiplied by each and every one of the monomials that form the polynomial. In other words, multiply the monomial with every term of the polynomial.
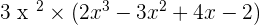


Multiplication of Polynomials
P(x) = 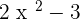 Q(x) =
Q(x) = 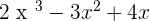
Multiply each monomial from the first polynomial by each of the monomials in the second polynomial.
P(x) · Q(x) = 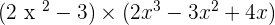

Add the monomials of the same degree:
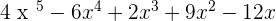
The multiplication of polynomials is another polynomial whose degree is the sum of the degrees of the polynomials that are to be multiplied.
Example
1. P(x) = 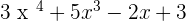 and Q(x) =
and Q(x) = 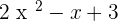
P(x) · Q(x) = 
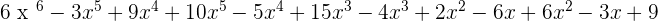
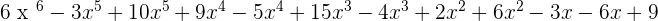
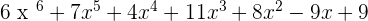
2. F(y) = 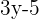 and G(y) =
and G(y) = 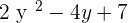
F(y) · G(y) = 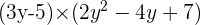

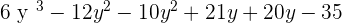
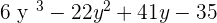
3. A(t) = 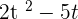 and B(t) =
and B(t) = 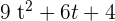
A(t) · G(t) = 
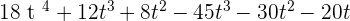
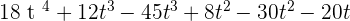
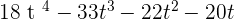
4. P(x) = 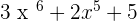 and Q(x) =
and Q(x) = 
P(x) · Q(x) = 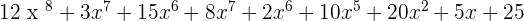
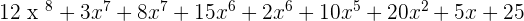

Summarise with AI:













