Chapters
What is a polynomial?
A polynomial is a mathematical expression made up of variables (like x or y), coefficients (numbers in front of variables), and exponents (whole numbers only). For example:
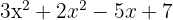
This is a polynomial in one variable (x). Polynomials are closed under addition, subtraction, and multiplication, which means combining polynomials with these operations always produces another polynomial.
What are polynomial word problems?
Polynomial word problems are real-life or practical problems that can be represented and solved using polynomials. They are super useful in modelling situations where quantities grow, shrink, or change.
In this article, we’ll practice solving different types of polynomial word problems, including finding unknown constants, factoring, determining roots, and applying this to real-life examples.
Polynomials are made of numbers and variables with whole-number powers.
They can have one or more terms (like 𝑥² + 3𝑥 + 2).
Polynomials are used in real life to model things like area, revenue, and distance.
Polynomial Word Problems Practice Questions
Find the best Maths tutors on Superprof.
Find a and b if the polynomial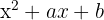 
is divisible by 
.
Step 1: Substitute 
into the polynomial to give 
Step 2: Simplify to 
Step 3: Solve for a and b 
Determine the value of m if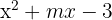 
has 
as one of its roots.
Step 1: Substitute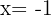 
into the polynomial 
Step 2: Simplify to 
Step 3: Solve for m 
Find a fourth-degree polynomial that is divisible by 
and has roots at and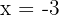 
.
Step 1: Identify roots 
Step 2: Write factors 
Step 3: Multiply by 
to make the fourth-degree 
Calculate the value of a for which the polynomial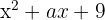 
has the root 
. Also, calculate the other root.
Step 1: Substitute into the polynomial 
Step 2: Simplify to 
Step 3: Solve for a 
Step 4: Write polynomial with found a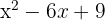 
Step 5: Factor polynomial 
The length of a rectangle is 
and its width is 
. Find the area of the rectangle.
Step 1: Multiply length and width 
Step 2: Simplify to 
The average number of tablets sold in a month t is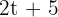 
and the price per tablet is 
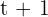. Find the total revenue at the end of 12 months.
Step 1: Multiply number sold and price 
Step 2: Substitute 
: 
Step 3: Simplify 
The area of a rectangle is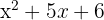 
and its length is . Find the width.
Step 1: Divide area by length
Step 2: Factor the numerator
Step 3: Simplify to
The distance covered by a cyclist is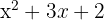 
and the time taken is 
. Find their speed.
Step 1: Divide distance by time to find speed
Step 2: Factor the numerator
Step 3: Simplify
A company sells speakers and headphones. The number of speakers sold is given by: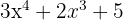 
, and the price per speaker expressed as: 
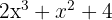. The number of headphones sold is given by: 
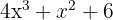, and the price per headphone expressed as: 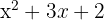. Find the polynomial to describe the total revenue.
Step 1: Calculate revenue from speakers 
Step 2: Calculate revenue from headphones 
Step 3: Combine the polynomials 
Did you like this article? Rate it!
Loading...
you do best but the best thing is helping us to i apprecite it
Hi Eyob! Thank you for your feedback! Great to hear that you’ve found these resources useful.
in this website math formulas not rendering properly??