Chapters
We write algebraic fractions as we write simple fractions with a numerator and denominator. The difference between a normal fraction and algebraic fraction is that the normal fraction usually contains numbers in numerator or denominator, while algebraic fractions have algebraic expressions in numerator and denominator. Algebraic fractions are basically the rational expressions which can be written in the following fractional form:
 where
where 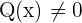
We simplify algebraic fractions in the same way as we simplify the normal fractions, i.e. numerator and denominator are divided by a common factor. The techniques for adding and subtracting algebraic fractions is also the same as the normal fractions. In this article, we will see how to simplify the fractions by adding, subtracting, multiplying and dividing them.
Let us start with addition.

1. Adding Algebraic Fractions
We take L.C.D to add two or more algebraic fractions when we have addition and subtraction sign between them. L.C.D stands for the least common denominator and the process of finding L.C.D is the same as the process of finding L.C.M of the fractions. L.C.D shows the smallest number divisible by the denominator of each fraction in the question. L.C.M is the least common multiple of two numbers.
The following examples will make this concept more clear.
Example 1
Add fractions 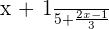
Solution
To add the above two fractions, take the L.C.D of 5 and 3.
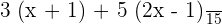
By multiplying 3 and 5 with the terms inside the brackets:
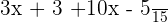
Now, combine the like terms and add or subtract them depending on their signs:
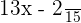
Since the above fraction cannot be simplified further, so 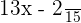 is the correct answer.
is the correct answer.
Example 2

Solution
the above algebraic expression is different than the first example because it contains algebraic expressions both in the numerator and the denominator. Take L.C.D of the expressions. We know that  .
.
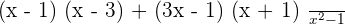
Use the FOIL method of multiplication to multiply the binomial terms in the numerator:
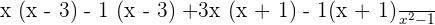
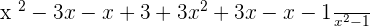
Combine the like terms together and apply their respective operations of addition or subtraction like this:
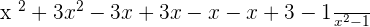
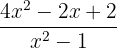
Since, the fraction 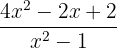 cannot be simplified further, so it is the final answer.
cannot be simplified further, so it is the final answer.
Example 3
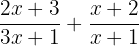
Solution
Take the L.C.D of the expressions and write the resultant expression as:
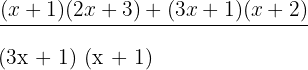
The terms in the numerators will be multiplied using the FOIL method:
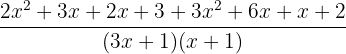
Add the like terms together:
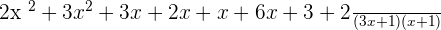
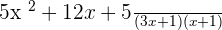
You can also use the FOIL method to multiply the terms in the denominator and write the resultant expression as:
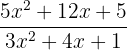
Since the above expression cannot be simplified further, so it is the final answer.
Find good maths tutors near me here.
2. Subtracting Algebraic Fractions
We subtract algebraic fractions in the same way as we add them. The only difference is when we apply the operation of subtraction after multiplication. The signs of all the factors inside the brackets are reversed because of the minus sign outside the bracket. Let us explain this concept through following examples
Example 1
Subtract fractions 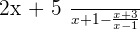
Solution
Take the L.C.D to write the expression as:
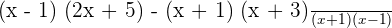
Since 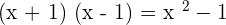 , so we will write the expression as:
, so we will write the expression as:
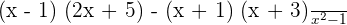
Use the FOIL method to multiply the terms in the numerator:
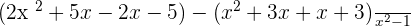
It is better to add or subtract the like terms together inside the parentheses before opening the brackets in the numerator:
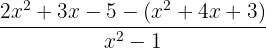
Open the bracket in the numerator and reverse the signs of the terms which were inside the parenthesis:
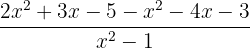
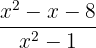
The above fraction cannot be simplified further, hence it is the final answer.
Example 2
Simplify 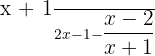
Solution
Take L.C.D of the denominators and write the expression as:
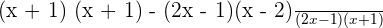
Use FOIL method to multiply the expressions:

Multiply the terms inside the brackets by variables and constant in the numerator:
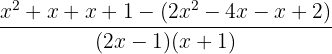
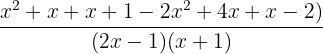
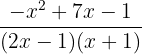
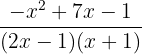
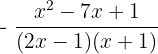
Example 3
Simplify 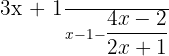
Solution
Taking L.C.D, we will write the above expression as:
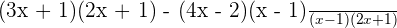
Use FOIL method to multiply the numerator:


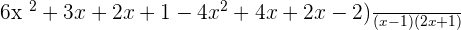
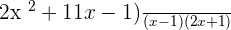
3. Multiplying Algebraic Fractions
Multiplying algebraic fractions is very simple. You just have to multiply the numerator with the numerator and denominator with the denominator. Let us explain the concept through the following examples.
Example 1

Solution
Multiply the numerators and the denominators together to simplify the above algebraic expression:
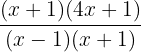
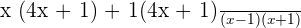
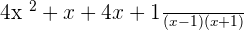
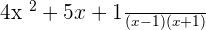
Factoring 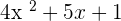 we will get the factors
we will get the factors 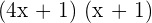 :
:
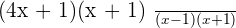
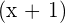 is the common factor both in the numerator and denominator, hence we will cancel out this factor and write the final answer as:
is the common factor both in the numerator and denominator, hence we will cancel out this factor and write the final answer as:

Example 2
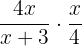
Solution
Multiplying the numerators and the denominators together will give the following expression:
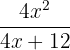
Remember that while writing the final answer simplifying fractions is necessary. Simplifying means reducing fractions to the lowest possible fraction. You can see that in the above expression,  is the common factor both in the numerator and the denominator. Hence, we will write the expressions as:
is the common factor both in the numerator and the denominator. Hence, we will write the expressions as:
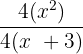
Cancel out  in the numerator and the denominator to write the above expression as a single fraction like this:
in the numerator and the denominator to write the above expression as a single fraction like this:
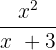
Example 3
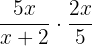
Solution
Multiplying the numerators and the denominators together will give us the following expression:
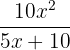
You can see that 5 is the common term in the numerator and the denominator:
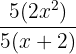
 will be cancelled out to write the final expression as:
will be cancelled out to write the final expression as:
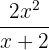
4. Dividing Algebraic Fractions
We divide algebraic fractions using the same process as we follow while dividing fractions, i.e. we take reciprocal of the second fraction. Let us explain the concept through the following examples.
Example 1
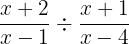
Solution
Take the reciprocal of the second fraction:
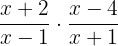
Multiply the numerators and denominators together:
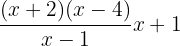
Example 2

Solution
Take the reciprocal of the second fraction:
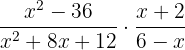
Factor the terms in the numerator and the denominator as much as possible:
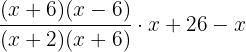
Write the resulting expression by cancelling out 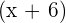 and
and 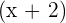 :
:
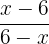
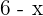 can be written as
can be written as  , hence the above expression can be simplified further as:
, hence the above expression can be simplified further as:
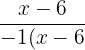
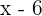 in the numerator and denominator will be cancelled out:
in the numerator and denominator will be cancelled out:

Hence, -1 is the simplest form of the above question.
Example 3
Simplify fractions 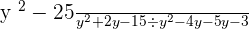
Solution
To divide, we will take the reciprocal of the second fractional expression. We will rewrite the above expression as:

Factor the expressions in the numerator and the denominator as much as possible:
Factoring of different fractions will yield following factors:
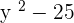 =
= 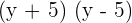

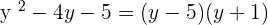
Write the expressions in factored form like this:
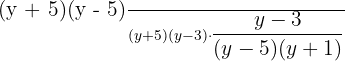
Cross multiply the two algebraic expressions to cancel out the common factors:
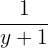
Hence, 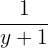 is in its simplest form.
is in its simplest form.
Summarise with AI:













