Chapters
Roots are those values which when substituted in a polynomial, evaluate the whole polynomial equal to zero. In other words, we can say that the root  set
set 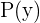 equal to zero. A polynomial can have multiple roots which means that many numbers can evaluate a polynomial equal to zero. In this article, we will discuss how to find the roots of a polynomial.
equal to zero. A polynomial can have multiple roots which means that many numbers can evaluate a polynomial equal to zero. In this article, we will discuss how to find the roots of a polynomial.

Remainder and Factor Theorem
In mathematics, the remainder and factor theorem are related to the roots or zeros of the polynomial. The reasoning for the factor and the remainder theorem is the same. The remainder theorem is explained below:
"The remainder theorem says that if you divide a polynomial P(y) by its factor x - b, then you will get a zero remainder."
The factor theorem is explained below:
- If P(z) is a polynomial of degree greater than 1 and b is any real number, then
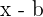 is a factor of the polynomial P(z), if and only if
is a factor of the polynomial P(z), if and only if 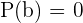 .
. 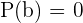 , if and only if
, if and only if 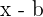 is the factor of the polynomial P(z). This value
is the factor of the polynomial P(z). This value 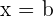 is the root or zero of the polynomial P(z).
is the root or zero of the polynomial P(z).
Roots of a Polynomial
These are the values that nullify the polynomial.
For example, if x - n is a factor of polynomial P(x), then x = n is the root or zero of the polynomial because when we will substitute the variables in the polynomial by the number n, then we will get 0. A polynomial can have more than one root.
Properties of the Roots and Factors of a Polynomial
- The zeros or roots are divisors of the independent term of the polynomial.
- For each root type x = a corresponds to it by a binomial of the type (x − a).
- A polynomial can be expressed in factors by writing it as a product of all the binomials of type (x − a), which will correspond to the roots, x = a.
- The sum of the exponents of the binomial must be equal to the degree of the polynomial.
- All polynomials that do not have an independent term accept x = 0 as a root.
- A polynomial is called irreducible or prime when it cannot be decomposed into factors.
Find the Roots and Factor the Following Polynomial
Example 1
Find the roots or zeros of the following polynomial:
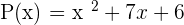
Solution
We will find the roots or zeros of the above polynomial by factoring the polynomial. We know how to factor a quadratic function. Because the above polynomial is of the form 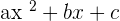 , hence it is a quadratic equation.
, hence it is a quadratic equation.
Factor the above quadratic function by following the procedure below:
- First, multiply the constant with the first term to get
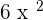 .
. - Now, expand the middle term in such a way that it adds up to the midterm
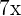 and multiplies together to get
and multiplies together to get 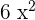 .
. - The first and third term will remain the same.
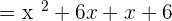
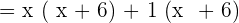
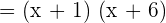
Now, set the factors equal to zero to find the roots of the polynomial like this:
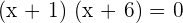
Either 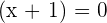 or
or 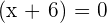 . Hence,
. Hence,  or
or  . This means that -1 and -6 are the roots or zeros of the polynomial. It means that when -1 and -6 will be substituted in the original polynomial equation, we will get 0.
. This means that -1 and -6 are the roots or zeros of the polynomial. It means that when -1 and -6 will be substituted in the original polynomial equation, we will get 0.
Example 2
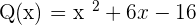
Solution
- First, multiply the constant with the first term to get
 .
. - Now, expand the middle term in such a way that it adds up to the midterm
 and multiplies together to get
and multiplies together to get 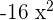 .
. - The first and third term will remain the same.
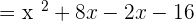
Now, pair first and second, and third and fourth terms and find common factors between them:
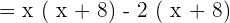
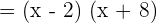
Set the above factors equal to zero:

Either,  or
or 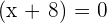 . Hence,
. Hence,  or
or 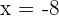 . It means that 2 and -8 are the roots or zeros of the polynomial, i.e. if they are substitute in the original polynomial equation, we will get the answer 0.
. It means that 2 and -8 are the roots or zeros of the polynomial, i.e. if they are substitute in the original polynomial equation, we will get the answer 0.
Example 3
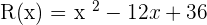
Solution
- First, multiply the constant with the first term to get
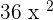 .
. - Now, expand the middle term in such a way that it adds up to the midterm
 and multiplies together to get
and multiplies together to get 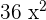 .
. - The first and third term will remain the same.

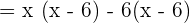
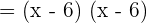
It means that the factor of the polynomial is 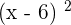 . To find the root set
. To find the root set 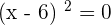 . Hence,
. Hence,  . This is an example of double root.
. This is an example of double root.
When we will substitute  in the original polynomial function, the resultant answer will be zero.
in the original polynomial function, the resultant answer will be zero.
Example 4

Solution
- First, multiply the constant with the first term to get
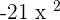 .
. - Now, expand the middle term in such a way that it adds up to the midterm
 and multiplies together to get
and multiplies together to get 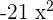 .
. - The first and third term will remain the same.
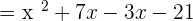
Pair the first and second, and third and fourth terms to find the common factors between them:

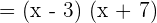
Set the factored form of the equation equal to zero:

Either,  or
or 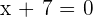 . Hence,
. Hence,  or
or  .
.
3 and -7 are the roots or zeros of the polynomial, which means if they are substituted in the above polynomial, we will get zero.
Example 5

Solution
- First, multiply the constant with the first term to get
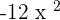 .
. - Now, expand the middle term in such a way that it adds up to the middle term
 and multiplies together to get
and multiplies together to get 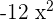 .
. - The first and third term will remain the same.

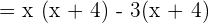
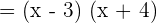
Set the factors equal to zero like this:

Either 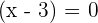 or
or 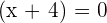 . Hence, x = 3 or x = -4. It means that 3 and -4 are the roots or zeros of the polynomial function. If we will substitute 3 or -4 in the original polynomial equation, we will get the answer 0.
. Hence, x = 3 or x = -4. It means that 3 and -4 are the roots or zeros of the polynomial function. If we will substitute 3 or -4 in the original polynomial equation, we will get the answer 0.
Find the best Maths tutors on Superprof.
Example 6
Given 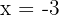 is the root of the polynomial
is the root of the polynomial 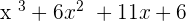 , find the other two factors.
, find the other two factors.
Solution
This example is different from the rest of the examples, as in this question we are given the root of the polynomial and we are asked to find the other two zeros. It also differs from the rest of the examples because the highest degree of the polynomial is 3 and there are four terms, hence we cannot find the factors using the same process as used in the previous examples.
We know that if 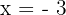 is the root of the polynomial, then the factor of the polynomial will be
is the root of the polynomial, then the factor of the polynomial will be  . The above polynomial should be completely divisible by
. The above polynomial should be completely divisible by  , if it is the factor of the polynomial. The complete divisibility means that the remainder should be 0. To find the other two factors, divide
, if it is the factor of the polynomial. The complete divisibility means that the remainder should be 0. To find the other two factors, divide 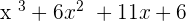 by
by  by long division method:
by long division method:
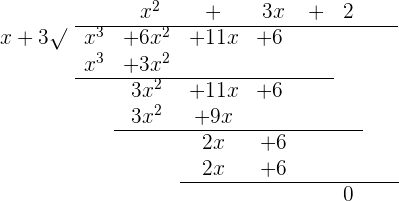
We know that the polynomial P(x) is equal to the product of its divisor and the quotient. Hence, the polynomial 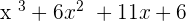 is equal to the product of the factor
is equal to the product of the factor 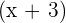 and the quotient
and the quotient  . We can write it mathematically as:
. We can write it mathematically as:

Factor the quotient using the following procedure:
- First, multiply the constant with the first term to get
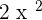 .
. - Now, expand the middle term in such a way that it adds up to the middle term
 and multiplies together to get
and multiplies together to get 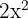 .
. - The first and third term will remain the same.
= 
Pair the first and second, and third and fourth terms together and find the common factors between them:


Set the factored form equal to zero:

Either  or
or  . Hence,
. Hence,  or
or  . It means that -2 and -1 are the zeros or roots of the quotient.
. It means that -2 and -1 are the zeros or roots of the quotient.
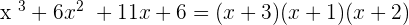
Therefore, there are 3 roots or zeros of the polynomial which are -3, -1 and -2.
Summarise with AI:













