
What is Denominator?
Whenever we talk about fractions, we usually are talking about numerator and denominator. So, what is the denominator? In maths, a denominator is a number that divides the numerator into equal parts.
For example, today is your birthday and you need to distribute the cake to your friends. The number of friends will be the denominator and the cake will be the numerator. Imagine you have 4 friends at your birthday party. This means you need to cut the cake in 4 equal parts. Let's convert it into the fraction, it will be " ". Each piece of cake will represent "
". Each piece of cake will represent " " and if you add the pieces of cake, it should give you 1 as your answer.
" and if you add the pieces of cake, it should give you 1 as your answer.

The denominator number doesn't matter. Even you need to cut your cake into 120 equal parts which might seem impossible in reality but maths can solve anything.
How To Reduce Algebraic Fractions to a Common Denominator
When you need to solve an algebraic fraction, you need to make sure that denominators are equal to each other. If all the denominators in algebraic fractions aren't equal, you can't apply any mathematical operations. In some cases, you might find the denominators are the same. If they are the same then you can apply given mathematical operations and if not then you need to reduce all the factions to a common denominator.
To reduce two algebraic fractions to a common denominator, find two equivalent algebraic fractions with the same denominator.
Example
1. 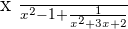
Step 1
Decompose the denominators to find the least common multiple, which will be the common denominator.
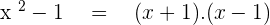
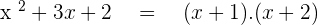 (After breaking the middle term and factorizing)
(After breaking the middle term and factorizing)
LCM (Least Common Multiple): 
To find the least common multiple, you need to multiply all the factors. If any factor is common then just write it one time like shown above. 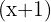 is the common factor in both denominators. That is why
is the common factor in both denominators. That is why 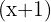 is written only one time.
is written only one time.
Step 2
This common denominator is divided by each of the denominators, multiplying the quotient obtained by the corresponding numerator.
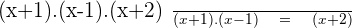
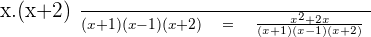
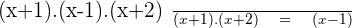
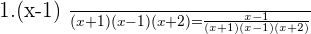
Step 3
Once you reduced all algebraic fractions to a common denominator now it is time to apply the mathematical operation.
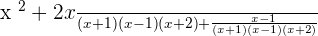
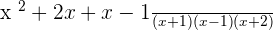
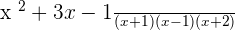
2. 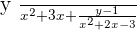
Step 1



Step 2

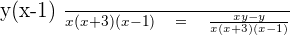


Step 3
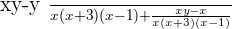
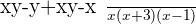

3. 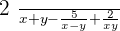
Step 1
LCM (Least Common Multiple): 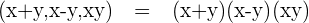
Step 2

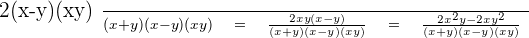
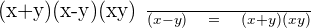
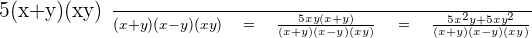
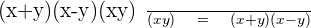
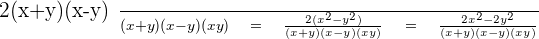
Step 3

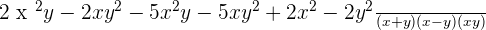
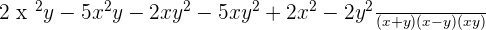
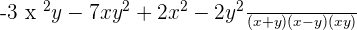

Check for maths tuition here.
Summarise with AI:













