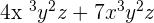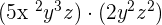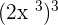Chapters

What are Monomials?
In algebra, monomials are the algebraic expressions having a single term only. As opposed to monomials, binomial contain two terms and a trinomial has three terms. Binomial and trinomial are also known as a polynomial. Polynomial is an algebraic expression that has multiple terms. In this article, we will focus on monomial expressions.
A monomial consists of constants and variables which may be multiplied together. Any individual number or variable is a monomial. For example, the number 3 and the variable x are monomials. If they are multiplied together, they will yield a monomial.
Remember that the exponent of the variable of a monomial term should be a whole number. It means that the terms 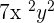 ,
, 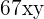 and
and 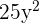 are all the examples of the monomials because the exponents are whole numbers. Whereas, the terms
are all the examples of the monomials because the exponents are whole numbers. Whereas, the terms 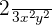 ,
,  and
and 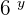 are not monomials.
are not monomials.
Let us see what some of the rules of monomials are.
Rules of Monomials
- When two monomials are multiplied together, we get another monomial. For example,
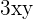 and
and 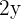 both are the monomials. If they are multiplied with each other, we will get another monomial
both are the monomials. If they are multiplied with each other, we will get another monomial 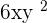 .
. - When a monomial is multiplied by a constant, we get a monomial term. For example, when a monomial term
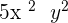 is multiplied by 3, we get another monomial term that is
is multiplied by 3, we get another monomial term that is  .
.
Remember that the multiple digit numbers like 23, 638, 1273, 23097 and 987365 are also monomials.
Degree of Monomials
The degree of a monomial term is found by adding the exponents of all the variables together in a monomial expression. Constants or numbers in the monomials have 0 degree. Let us understand this by the examples presented in the table below:
| Monomials | Degree |
|---|---|
| 1 + 2 + 2 = 5 | |
| 5 + 4 = 9 | |
| 3 + 2 + 3 = 8 | |
| 6 + 3 = 9 |
Addition of Monomials
Rules for Adding Monomials
- Similar monomials can be added. The sum of the monomials is another monomial that has the same literal part and whose coefficient is the sum of the coefficients.
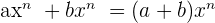
- A polynomial expression is obtained if monomials are not similar.
Examples
These monomials are similar, i.e. they have the same exponents. The only difference between these two monomials is that they have different numbers. To write an answer, we will just add the numbers up and write the answer as:
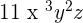
You can see that the resultant answer is also a monomial.
2. 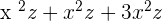
The above monomial terms are similar. They have the same variables and their powers, hence we will write the answer as:

3. 
The above monomial terms are not similar, i.e. the exponents are different, hence we will solve the above example like this:

Since 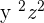 is the common factor in all the three terms, so we can write the above trinominal as follows after factoring:
is the common factor in all the three terms, so we can write the above trinominal as follows after factoring:
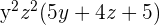
4. 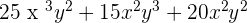
The monomials in this example are also not similar, hence we will solve the example like this:
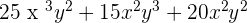
Since  is the common factor of all the above monomial terms, hence we will write the final answer as follows:
is the common factor of all the above monomial terms, hence we will write the final answer as follows:

Subtraction of Monomials
Rules for Subtracting Monomials
The rules for subtracting monomials are the same as the rules for adding monomials:
- Similar monomials can be subtracted. The difference of the monomials is another monomial that has the same literal part and whose coefficient is the difference of the coefficients.
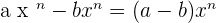
- A polynomial is obtained if monomials are not similar.
Examples
In the above example, the powers of the variables are the same, hence we will subtract the coefficients of the variables and write the final answer like this:
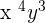
2. 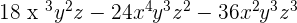
In the above examples, the powers of the variables of all the monomial terms are different. 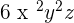 is the common factor in all the monomials. Hence, we will write the final answer as:
is the common factor in all the monomials. Hence, we will write the final answer as:
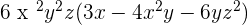
When the monomials involve addition or subtraction sign, it is better to write the final answer by factoring out the common term.
Multiplication of a Number by a Monomial
The product of a number by a monomial is another similar monomial whose coefficient is the product of the coefficient of the monomial and the number.
Examples
1. 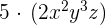
5 in the above monomial will be multiplied by the coefficient of the monomial which is 2. The answer will be the following monomial term:
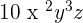
2. 
The number 7 in the above example will be multiplied by the coefficient of the monomial inside the parentheses. The answer will be a monomial term and will be written like this:
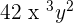
Multiplication of Monomials
The addition and subtraction of monomials are simple. Multiplication and division of monomials involve the laws of exponents. Let us see how to solve the monomials when they have a multiplication or division sign between them. The multiplication of monomials is another monomial that takes as its coefficient the product of the coefficients and whose literal part is obtained by multiplying the powers that have the same base. According to the laws of exponents, we multiply the exponents by adding their powers together in the answer.
The general notation of multiplication of monomials is given below:

Examples
The coefficients 5 and 2 of the above monomial terms will be multiplied together to obtain 10. Whereas, the powers having the same base will be added together like this:

Since the second monomial has no  , so we will assume the power of
, so we will assume the power of  in the second monomial is 0.
in the second monomial is 0.
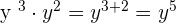

Hence,after simplifying the final answer will be written as:

2. 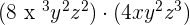
Multiply 8 and 4 together to get the number 32. The powers of the variables will be added as follows:
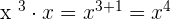
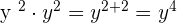
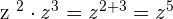
The final answer will be 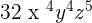 .
.
3. 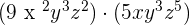
Multiply 9 and 5 together to get the answer 45. The powers of the same variables will be added as follows:
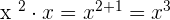

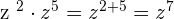
Hence, the final answer will be written like this:
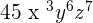
Division of Monomials
Division in monomials can only be performed if they have the same literal part and the degree of the dividend has to be greater than or equal to the corresponding divisor.
Rules for Diving Monomials
- The division of monomials is another monomial whose coefficient is the quotient of the coefficients and its literal part is obtained by dividing the powers of the same variables. According to the law of exponents, when we divide exponents having the same bases, we subtract the exponents while writing the answer.
- If the degree of the divisor is greater than the dividend, then the division of the monomials generate algebraic expressions.
The mathematical notation of the division of monomials is written as follows:

Examples
1. 
6 divided by 3 is equal to 2. The powers of the remaining variables will be calculated as follows:
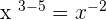
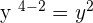

Combine the coefficient and all the variables together to write the final answer:
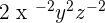
The negative exponents in the numerator or denominator can be made positive by taking its reciprocal, hence to simplify we will take the reciprocal of the variables with negative powers:
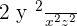
Since, the degree of two variables of the divisor was greater than the degree of those variables in the dividend, so an algebraic expression is obtained in the above example.
2. 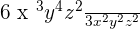
6 will be divided by 3 to get 2. The remaining variables will be obtained as follows:
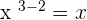
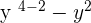
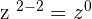
Combine the coefficient and the variables together to write the final answer as follows:
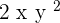
3. 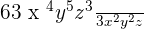
63 will be divided by 3 to get 21. The powers of the remaining exponents will be obtained as follows:
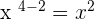
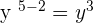
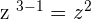
Combine the constant and the variables together to write the final answer as:
Find the best Maths tutor on Superprof.
Power of a Monomial
To determine the power of a monomial, every element in the monomial is raised to the exponent of the power. The general notation is written below:
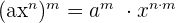
Examples
The constant will be raised to the power 3 and the power of the variable inside the brackets will be multiplied by the power outside the parentheses. Hence, the final answer will be written as:

2. 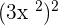
Take square of the number -3 and multiply the power 2 of the variable by the power of the expression outside the brackets . Hence, the resultant answer will be written as follows:
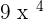
3. 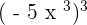
Take cube of the number and multiply 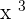 by 3 to make it
by 3 to make it 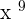 . Hence, the resulting answer will be written as follows:
. Hence, the resulting answer will be written as follows:
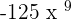
Summary of Arithmetic Operations with Monomials
The summary table of operations of all the monomials is given below:
| Operation | General notation of a monomial |
|---|---|
| Addition | |
| Subtraction | |
| Multiplication | |
| Division | |
| Power |
Summarise with AI: