Chapters
- Exercise 1
- Exercise 2
- Exercise 3
- Exercise 4
- Exercise 5
- Exercise 6
- Exercise 7
- Solution of exercise Algebraic Fractions Worksheet
- Solution of exercise 1
- Solution of exercise Algebraic Fractions Worksheet
- Solution of exercise 2
- Solution of exercise Algebraic Fractions Worksheet
- Solution of exercise 3
- Solution of exercise Algebraic Fractions Worksheet
- Solution of exercise 4
- Solution of exercise Algebraic Fractions Worksheet
- Solution of exercise 5
- Solution of exercise Algebraic Fractions Worksheet
- Solution of exercise 6
- Solution of exercise Algebraic Fractions Worksheet
- Solution of exercise 7

Exercise 1
Simplify:
1 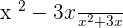
2 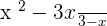
3 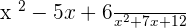
4 
5 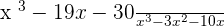
Exercise 2
Calculate:
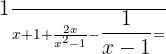
Exercise 3
Calculate:
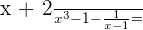
Exercise 4
Calculate:
1 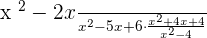
2 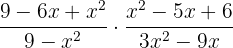
Exercise 5
Calculate:
1 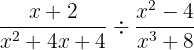
2 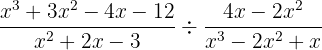
Exercise 6
Calculate:
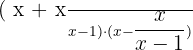
Exercise 7
Calculate:
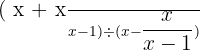
Find the best Maths tutor on Superprof.
Solution of exercise Algebraic Fractions Worksheet
Solution of exercise 1
Simplify:
1 
 is the factor both in the numerator and the denominator:
is the factor both in the numerator and the denominator:
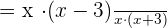
Cancel  from the numerator and the denominator:
from the numerator and the denominator:
=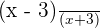
2 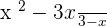
 is the common factor in the numerator and the denominator:
is the common factor in the numerator and the denominator:

Make it  :
:

Cancel  from both the numerator and denominator. The resultant answer will be
from both the numerator and denominator. The resultant answer will be  .
.
3. 
Factorize the numerator and the denominator:
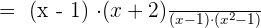
 will be cancelled from both numerator and the denominator:
will be cancelled from both numerator and the denominator:
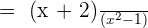
3 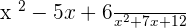
Factorize the numerator and the denominator:
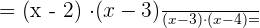
Cancel  from both numerator and the denominator:
from both numerator and the denominator:

4 
Factorize the numerator and the denominator:

Cancel  from the numerator and the denominator:
from the numerator and the denominator:
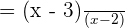
5 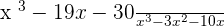
Factorize the numerator and the denominator:

The common factors will be cancelled:
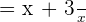
Solution of exercise Algebraic Fractions Worksheet
Solution of exercise 2
Calculate:
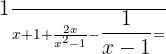
Take L.C.D of the above expression:

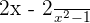
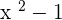 can be written as
can be written as 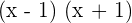 :
:
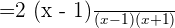
 will be cancelled from both the numerator and the denominator. Hence, the resultant answer will be:
will be cancelled from both the numerator and the denominator. Hence, the resultant answer will be:
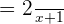
Solution of exercise Algebraic Fractions Worksheet
Solution of exercise 3
Calculate:
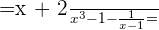
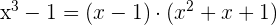
Least Common Denominator ( L.C.D) is 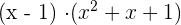
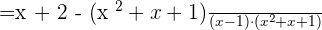
The parentheses in the numerator will be opened and the signs of all the terms inside it will be reversed:


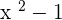 can be factored as
can be factored as 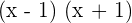
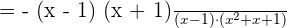
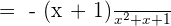
Solution of exercise Algebraic Fractions Worksheet
Solution of exercise 4
Calculate:
1 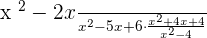



2 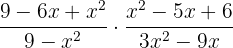
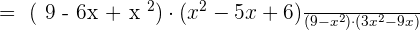

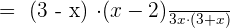
Solution of exercise Algebraic Fractions Worksheet
Solution of exercise 5
Calculate:
1 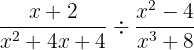
The second expression will be reversed because of the division sign:
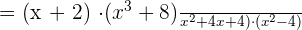
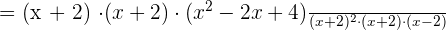

2 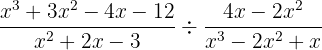
The second fraction will be reversed because of the division sign:

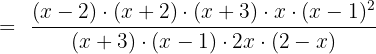

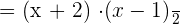
Solution of exercise Algebraic Fractions Worksheet
Solution of exercise 6
Calculate:
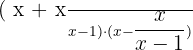
Since, 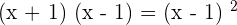 , so
, so 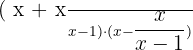 can be written as:
can be written as:
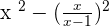
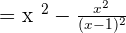
Take L.C.D of both the expressions:
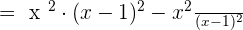
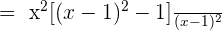
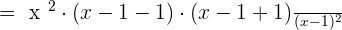
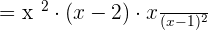
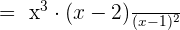
Solution of exercise Algebraic Fractions Worksheet
Solution of exercise 7
Calculate:
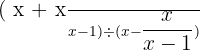
Take L.C.D of the second expression:
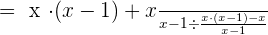
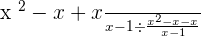
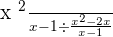

Summarise with AI:













