Chapters
In this article, you will learn how to calculate the volume of a function using integration. But before proceeding to discuss the volume of a function by integration method, first, let us recall the integration concept.

What is Integration?
The integration of a function represents the summation of discrete data. The integral is computed to find the functions which denote area, volume, or displacement. These functions have a collection of small data, hence they cannot be measured separately. Generally, in calculus, we use limits or boundaries where we are dealing with algebra and geometry. Limits enable us to study the result of points on the graph as to how much they get near to one another until the distance almost becomes zero.
Calculus is divided into two main categories:
- Differential Calculus
- Integral Calculus
The concept of integration is included in the integral calculus and it is the reverse process of differentiation. It helps us to solve the following two types of problems:
- Determining the problem function when the derivatives are given.
- Finding the area bounded by the graph of a function under certain conditions known as constraints
These two types of problems are the crux of integral calculus. Integral calculus further contains definite and indefinite integral. In calculus, the differentiation and integration of a given function are linked using a theorem known as the Fundamental Theorem of Calculus.
In the next section, we will discuss how to determine the volume of a function using the integration technique.
Volume of a Function
We can also utilize the definite integral to determine the volume of a solid. This volume is obtained through a revolution of a plane region about the vertical or horizontal line that does not cross through the plane. This kind of solid will be composed of three types of elements: disks, washers, or cylindrical shells. Each of these elements needs a unique approach in setting up a definite integral to find the volume. We have discussed each approach along with the examples below.
Disk Method
We can use the disk method to calculate the volume of a solid when the axis of revolution is the boundary of the plane region and cross-sections are perpendicular to this axis of revolution. This is due to the fact that the cross section of a disk is a circle having the area 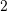 . The volume of each disk is equal to the product of the area and its thickness. When a disk is perpendicular to the x-axis, then the radius should be defined as a function of x. In case, the disk is perpendicular to the y-axis, the radius should be defined as a function of y.
. The volume of each disk is equal to the product of the area and its thickness. When a disk is perpendicular to the x-axis, then the radius should be defined as a function of x. In case, the disk is perpendicular to the y-axis, the radius should be defined as a function of y.
We denote the volume (V) of a solid obtained by revolving the region bounded by y = f(x) and the x-axis on the closed interval [a, b] about the x-axis like this:
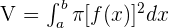
On the other hand, the volume (V) of a solid obtained by revolving the region bounded by x = f(y) and the y-axis on the closed interval [a, b] about the y-axis is denoted like this:

Example 1
Find the volume of the solid obtained by rotating the region bounded by 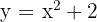 , x = 0, x = 1, and the x-axis about the x-axis.
, x = 0, x = 1, and the x-axis about the x-axis.
Solution
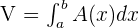
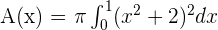
The antiderivative of 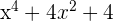 is
is 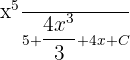 .
.
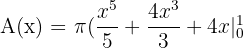
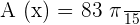
Example 2
Find the volume of the solid obtained by rotating the region bounded by 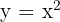 , x = 3, x = 4, and the x-axis about the x-axis.
, x = 3, x = 4, and the x-axis about the x-axis.
Solution
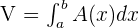

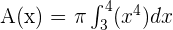
The antiderivative of  is
is  .
.
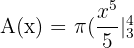
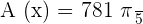
Washer Method
We use a washer method when the axis of the revolution is not a boundary of the plane region and cross-sections are perpendicular to the axis of revolution. Consider a washer as a "disk with a hole in it" or as a disk with a disk eliminated from the center. Consider that R is the radius of the outer disk and r as the radius of the inner disk. In this case, the area of the washer is 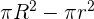 , and its volume will be the product of the area and its thickness.
, and its volume will be the product of the area and its thickness.
The volume V of a solid produced by revolving the region bounded by y = f(x) and y = g(x) on the closed interval [a, b], where  , about the x-axis is:
, about the x-axis is:
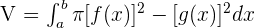
When the region is bounded by x = f(y) and x = g(y) on the closed interval [a, b], where  is revolved about the y-axis, then its volume (V) is given by:
is revolved about the y-axis, then its volume (V) is given by:
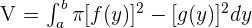
Example 1
Calculate the volume of the solid produced by revolving the region bounded by 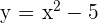 and
and 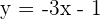 about the x-axis.
about the x-axis.
Solution
First, we will find the boundaries by equating both the functions as shown below:
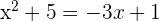

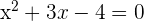


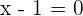 or
or 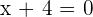
 or
or 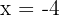
Now, we will use the above boundaries and the two functions to write the functions in the following form:
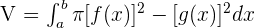
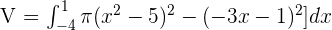
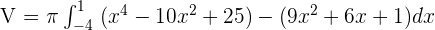
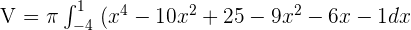


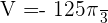
Cylindrical Shell Method
When the cross sections of the solid are given parallel to the axis of revolution, then we use the cylindrical shell technique to determine the volume of a solid. If the radius of the cylindrical shell is r and height h, then its volume will be equal to the product of 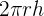 and its thickness.
and its thickness.
The volume V of a solid produced by revolving the region bounded by the function y = f(x) and the x-axis on the closed interval [a, b], where 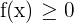 about the y -axis is given by:
about the y -axis is given by:
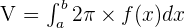
The volume V of a solid produced by revolving the region bounded by the function x = f(y) and the y-axis on the closed interval [a, b], where 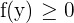 about the y -axis is given by:
about the y -axis is given by:
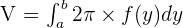
Example
What is the volume of the solid produced by revolving the region bounded by 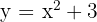 and the x‐axis [2,1] about the y‐axis?
and the x‐axis [2,1] about the y‐axis?
Solution



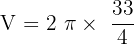
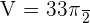
Summarise with AI:













