Chapters
- Exercise 1
- Exercise 2
- Exercise 3
- Exercise 4
- Exercise 5
- Exercise 6
- Exercise 7
- Exercise 8
- Exercise 9
- Exercise 10
- Exercise 11
- Solution of exercise 1
- Solution of exercise 2
- Solution of exercise 3
- Solution of exercise 4
- Solution of exercise 5
- Solution of exercise 6
- Solution of exercise 7
- Solution of exercise 8
- Solution of exercise 9
- Solution of exercise 10
- Solution of exercise 11
Calculate the following integrals:

The best Maths tutors available
Exercise 1
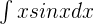
Exercise 2
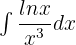
Exercise 3
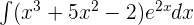
Exercise 4
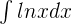
Exercise 5

Exercise 6
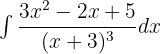
Exercise 7
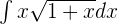
Exercise 8
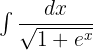
Exercise 9
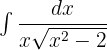
Exercise 10

Exercise 11
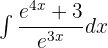
Solution of exercise 1


Solution of exercise 2
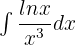
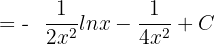
Solution of exercise 3
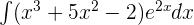
If  , then
, then 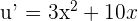 .
.
If 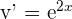 , then
, then 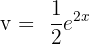
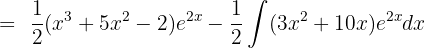
Suppose 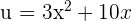 , then
, then 
If 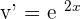 , then
, then 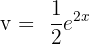
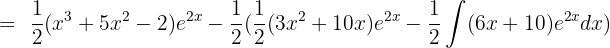
If u = 6x + 10, then u' = 6
If v' =  , then
, then 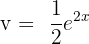
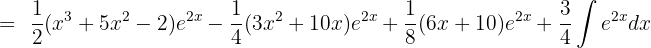
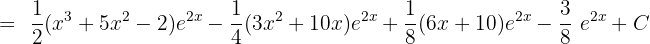
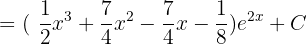
Solution of exercise 4
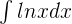
If u = lnx, then 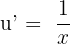
If v' = 1, then v = x
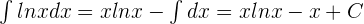
Solution of exercise 5
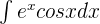
If  , then
, then 
If v' = cos x, then v = sin x
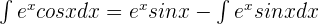
If  , then
, then 
If v' = sin x, then v = -cos x
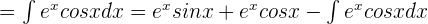

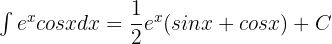
Solution of exercise 6
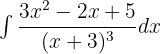
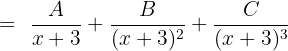

To calculate A, B and C, we substitute x with −3:
Derive and replace with −3:
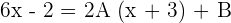

x = -3 -20 = B
Derive again:
6 = 2A A = 3
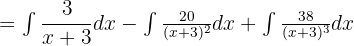
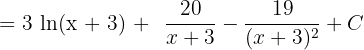
Also, the coefficients can be found by realizing the operations and equaling coefficients:
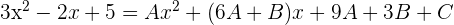
-2 = 19 + B
5 = 27 + C
3 = A
B = -20
C = 38
Solution of exercise 7
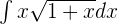
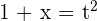


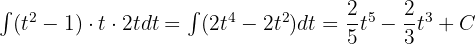
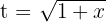
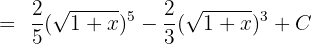
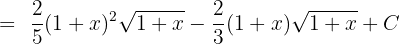
Solution of exercise 8
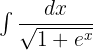
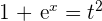
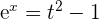
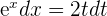
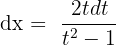
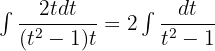
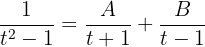
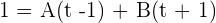
t = -1 1 = -2A A = 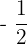
t = 1 1 = 2B B = 
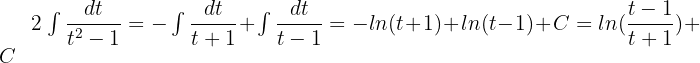
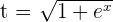
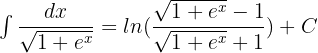
Solution of exercise 9
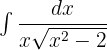
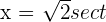
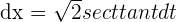
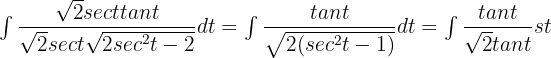
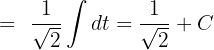
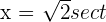
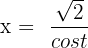
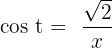
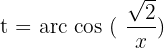
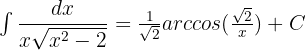
Solution of exercise 10

= 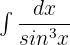
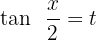
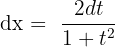
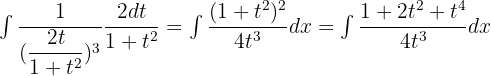
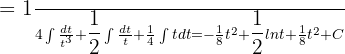
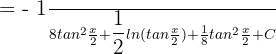
Solution of exercise 11
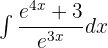
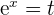

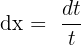
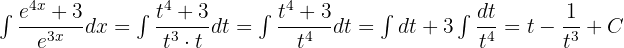
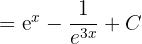
Summarise with AI:













