Chapters

Introduction
In this article, we will discuss how to find the integral of an exponential function. But, first, let us see what is meant by integration.
Integration is one of the most important concepts of calculus and it is the reverse process of differentiation. It represents the summation of discrete data and it is calculated to find functions describing volume, area, and displacement. These functions cannot be measured singularly because they have a collection of discrete data.
What are Exponential functions?
Logarithmic and exponential functions are employed to model the growth of the population, and cells, etc. They are also used to model radioactive decay, depreciation, and resource consumption, etc. Exponential functions are the functions in which the independent variable "x" is the exponent or power of the base.
Integral of Exponential Function
The following two formulas are used as the basis of integrating an exponential function:
- The exponential function
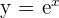 is its own derivative and integral. The integral of this function is:
is its own derivative and integral. The integral of this function is:
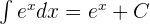
- The integral of the exponential function
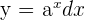 is given below:
is given below:
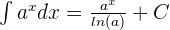
In the next section, you will find a list of integration rules that are quite helpful in finding the integrals of exponential functions:
Rules of Integration
Like differentiation, there are some rules which are used to solve the problems related to integration. These rules are explained below:
- Integration of a Constant
The integral of 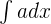 is equal to ax + C.
is equal to ax + C.
- Integration Power Rule
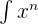 dx is equal to
dx is equal to 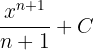
- Integration Sum Rule
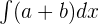 is equal to
is equal to  a dx +
a dx +  b dx
b dx
- Integration Difference Rule
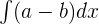 is equal to
is equal to  a dx -
a dx -  b dx
b dx
- Multiplication by Constant
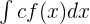 is equal to
is equal to 
Now, we will see how to solve problems involving the integration of the exponential functions.
Example 1
Find the integral of the following exponential function:
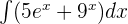
Solution
First, we will use the integral sum rule to write the above function separately like this:

Now, we will use the integral constant rule to shift the constant on the left side of the integral sign in the first term:
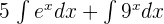
We know that 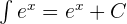 and
and 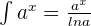 . We will use these two formulas to integrate both the terms like this:
. We will use these two formulas to integrate both the terms like this:
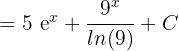
Example 2
Find the integral of the following exponential function:

Solution
We will solve this question by using the substitution method. Suppose  . This means that
. This means that  and
and 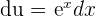 . Substitute these values in the above equation to get the following:
. Substitute these values in the above equation to get the following:
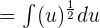
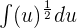 ios equal to
ios equal to 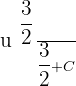
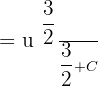
We will simplify it further to get the following:
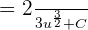
Substitute  back again the above equation to get the final answer:
back again the above equation to get the final answer:
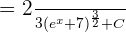
Example 3
Find the integral of the following exponential function:
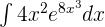
Solution
We will solve this question by using the substitution method. Suppose 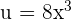 . It means that
. It means that 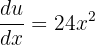 and
and 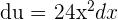 . Since, the original function contains
. Since, the original function contains  , not
, not 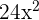 , so we will divide
, so we will divide 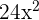 by 6. It will give us
by 6. It will give us 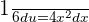 . Hence, we can write the equation by substituting these values like this:
. Hence, we can write the equation by substituting these values like this:
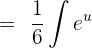
Now, we will integrate  as shown below:
as shown below:
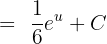
Substitute 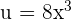 again in the above equation to get the following answer:
again in the above equation to get the following answer:
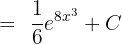
Example 4
Find the integral of the following exponential function:
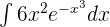
Solution
We will solve this example through substitution. Suppose 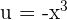 . Then,
. Then, 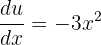 . This means that
. This means that 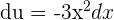 .
.
Since, the original function contains 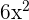 , not
, not 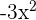 , so we will multiply
, so we will multiply 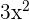 by 2. It will give us
by 2. It will give us  . Hence, we can write the equation by substituting these values like this:
. Hence, we can write the equation by substituting these values like this:
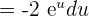
Now, we will integrate  as shown below:
as shown below:

Substitute 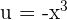 again in the above equation to get the following answer:
again in the above equation to get the following answer:
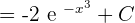
Example 5
Find the integral of the following exponential function:
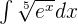
Solution
We will rewrite the above function in radical form like this:
= 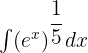
= 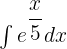
Now, we will use the substitution method to solve the above equation. Suppose 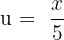 . This means that
. This means that 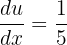 . Then,
. Then, 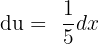 and
and 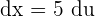
= 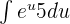
We will shift the constant before the integral sign:
= 
= 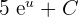
Substitute 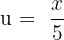 in the above equation again to get the following answer:
in the above equation again to get the following answer:
= 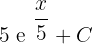
Example 6
Find the integral of the following exponential function:
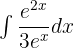
Solution
Shift the fraction to the left side of the integral sign like this:
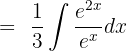
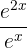 is equal to
is equal to  :
:
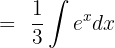
We can simply integrate this function because 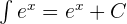 .
.
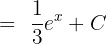
Example 7
Find the integral of the following exponential function:
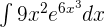
Solution
We will solve this question by using the substitution method. Suppose 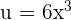 . It means that
. It means that 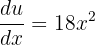 and
and 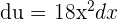 . Since, the original function contains
. Since, the original function contains  , not
, not  , so we will divide
, so we will divide  by 2. It will give us
by 2. It will give us 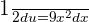 . Hence, we can write the equation by substituting these values like this:
. Hence, we can write the equation by substituting these values like this:
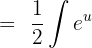
Now, we will integrate  as shown below:
as shown below:
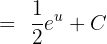
Substitute 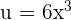 again in the above equation to get the following answer:
again in the above equation to get the following answer:
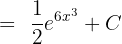
Example 8
Find the integral of the following function:
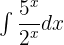
Solution
We can rewrite the above function like this:
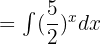
Remember the exponent integral formula 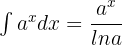 . We will apply this formula to the above function like this:
. We will apply this formula to the above function like this:
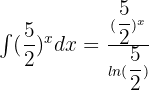
We will simplify the above equation to write the answer like this:
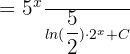













Hi,
what is the integral of ;
(k ^ -u x e ^ u)
Thanks,