In this article, we will discuss what is the average value of a function and how to calculate it.
An average value of a function is one of the primary applications of definite integrals. For computing the average value of a function, we use the "Fundamental Theorem of Calculus" to integrate the function and then we divide the value by the length of the interval.
The average value of a function f(x) over the closed interval [a,b] can be calculated using the formula below:
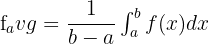
The average value of the function can also be calculated using mean value theorem. The mean value theorem says that if f(x) is a continuous function on the closed interval [a,b], then there is number c in the closed interval [a,b] in such a way that:
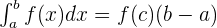
Now, we will solve some examples in which we will calculate an average value of the given functions.
Example 1
Find the average value of the following function on the interval [0, 2].
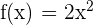
Solution
We will use the following formula to calculate the average value of the function:
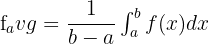
In this example, the value of b is 2 and a is 0. Now, substitute these values in the above equation like this:
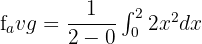
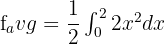
To integrate the function 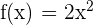, first, we will find the antiderivative of the function. The antiderivative of this function is 
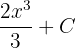. Suppose C = 0. The fundamental theorem of calculus says that:
Substitute 2 and 0 in the antiderivative of the function like this:
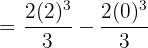
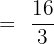
Hence, our definite integral is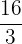 
. Now, we will substitute this value in the equation below like this:
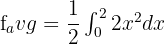
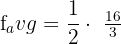
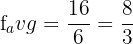
Hence, the average value of the function at the interval [0,2] is 
.
Example 2
Find the average value of the following function on the interval [0, 3].
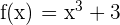
Solution
We will use the following formula to calculate the average value of the function:
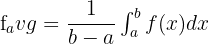
In this example, the value of b is 3 and a is 0. Now, substitute these values in the above equation like this:
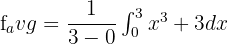
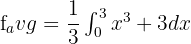
To integrate the function 
, first, we will find the antiderivative of the function. The antiderivative of this function is 
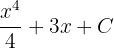. Suppose C = 0. The fundamental theorem of calculus says that:
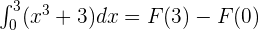
Substitute 3 and 0 in the antiderivative of the function like this:
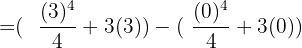
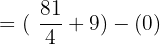
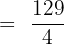
Hence, our definite integral is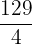 
. Now, we will substitute this value in the equation below like this:
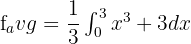
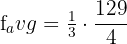
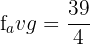
Hence, the average value of the function at the interval [0, 3] is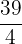 
.
Example 3
Find the average value of the following function on the interval [2,3].
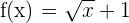
Solution
We will use the following formula to calculate the average value of the function:
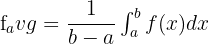
In this example, the value of b is 3 and a is 2. Now, substitute these values in the above equation like this:
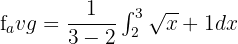
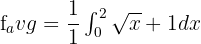
To integrate the function 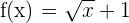, first, we will find the antiderivative of the function. The antiderivative of this function is 
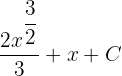. Suppose C = 0. The fundamental theorem of calculus says that:
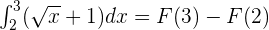
Substitute 3 and 2 in the antiderivative of the function like this:
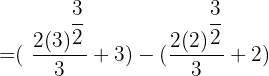
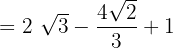
Hence, our definite integral is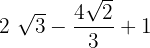 
. Now, we will substitute this value in the equation below like this:
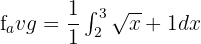
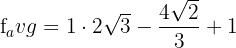
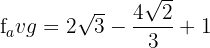
Hence, the average value of the function at the interval [2,3] is 2 \sqrt{3} - \frac{4 \sqrt{2}}{3} + 1.
Example 4
Find the average value of the following function on the interval [2, 4].
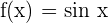
Solution
We will use the following formula to calculate the average value of the function:
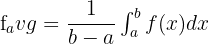
In this example, the value of b is 4 and a is 2. Now, substitute these values in the above equation like this:
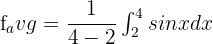
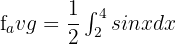
To integrate the function 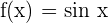, first, we will find the antiderivative of the function. The antiderivative of this function is - cos x + C. Suppose C = 0. The fundamental theorem of calculus says that:
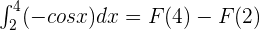
Substitute 4 and 2 in the antiderivative of the function like this:
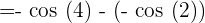
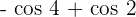
Hence, our definite integral is - cos 4 + cos 2. Now, we will substitute this value in the equation below like this:
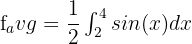
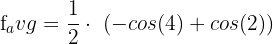
Hence, the average value of the function at the interval [2,4] is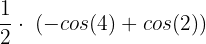 
.
Example 5
Find the average value of the following function on the interval [0, 5].
Solution
We will use the following formula to calculate the average value of the function:
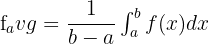
In this example, the value of b is 5 and a is 0. Now, substitute these values in the above equation like this:
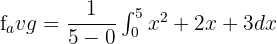
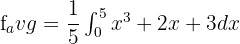
To integrate the function , first, we will find the antiderivative of the function. The antiderivative of this function is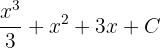 
. Suppose C = 0. The fundamental theorem of calculus says that:
Substitute 5 and 0 in the antiderivative of the function like this:
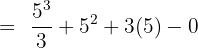
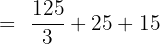
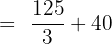
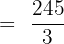
Hence, our definite integral is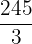 
. Now, we will substitute this value in the equation below like this:
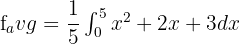
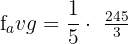
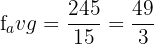
Hence, the average value of the function at the interval [0,5] is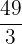 
.
Did you like this article? Rate it!
Loading...
Hi,
what is the integral of ;
(k ^ -u x e ^ u)
Thanks,