Chapters
Exercise 1
Find the volume of the solid obtained by rotating the region bounded by y = sen x, x = 0 and x = π and the x-axis about the x-axis.
Exercise 2
Calculate the volume of the cylinder generated by the rectangle bounded by straight lines y = 2, x = 1, x = 4, and the x-axis to rotate around the x-axis.
Exercise 3
Find the volume of the truncated cone generated by the trapezoid contained by the x-axis, the lines y = x + 2, x = 4 and x = 10, which turns around the x-axis.
Exercise 4
Find the volume generated by rotating the region bounded by y = 2x − x² and y = −x + 2 around the x-axis.
Exercise 5
Find the volume generated by rotating the region bounded by y²/8 = x and x = 2, around the y-axis.
Exercise 6
Calculate the volume of a sphere of radius r.
Exercise 7
Find the volume of the ellipsoid generated by the ellipse 16x² + 25y² = 400 and turning:
1 Around its major axis.
2 Around its minor axis.
Solution of exercise 1
Find the volume of the solid obtained by rotating the region bounded by y = sen x, x = 0 and x = π and the x-axis about the x-axis.
y = sen xx = 0x = π
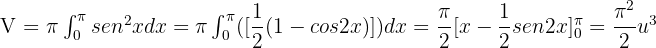
Solution of exercise 2
Calculate the volume of the cylinder generated by the rectangle bounded by straight lines y = 2, x = 1, x = 4, and the x-axis to rotate around the x-axis.
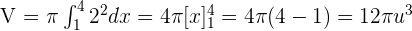
Solution of exercise 3
Find the volume of the truncated cone generated by the trapezoid contained by the x-axis, the lines y = x + 2, x = 4 and x = 10, which turns around the x-axis.
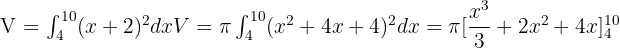
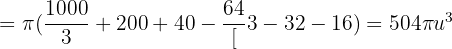
Solution of exercise 4
Find the volume generated by rotating the region bounded by y = 2x − x² and y = −x + 2 around the x-axis.
The points of intersection between the parabola and the line:
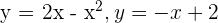
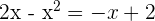
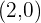
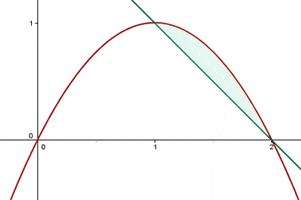
The parable is above the line in the interval of integration.
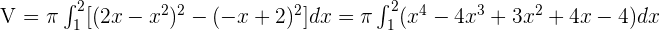
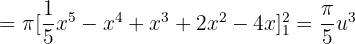
Solution of exercise 5
Find the volume generated by rotating the region bounded by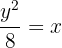 
and x = 2, around the y-axis.
As it turns about the y-axis, apply:
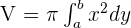
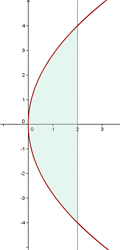
Since the parabola is symmetrical about the x-axis, the volume is equal to two times the volume generated between y = 0 and y = 4.
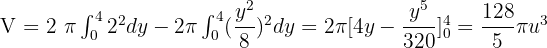
Solution of exercise 6
Calculate the volume of a sphere of radius r.
Start from the equation of the circumference x² + y² = r².
Turning a semicircle around the x-axis gives a sphere.
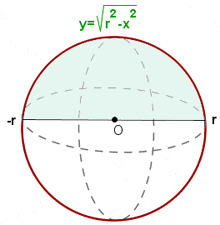
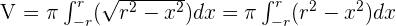
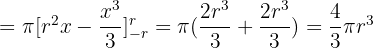
Solution of exercise 7
Find the volume of the ellipsoid generated by the ellipse 16x² + 25y² = 400 and turning:
1 Around its major axis.
2 Around its minor axis.
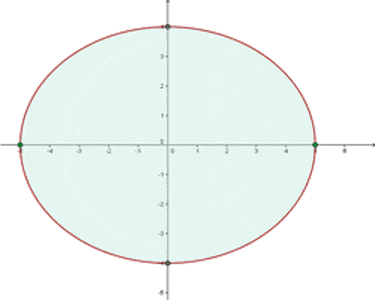
As the ellipse is symmetric about two axes, the volume is double the portion generated by the ellipse in the first quadrant in both cases.
Summarise with AI:
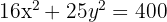
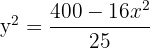
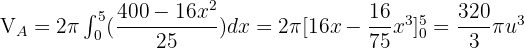
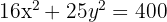
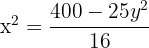
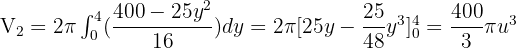
Did you like this article? Rate it!
Loading...
