Chapters

Integration Notation
As a reminder, integration notation is important to understand. There are two main integrals you will encounter:

| A | B | C | |
| Indefinite | Integral without bounds | Function | Variable to be integrated |
| Definite | Integral with upper bound m and lower bound n | Function | Variable to be integrated |
In the table above, you can see that the only difference between indefinite and definite variables is that definite variables specify the interval for which the area needs to be calculated.
| A | B | C |
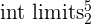 | 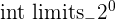 |  |
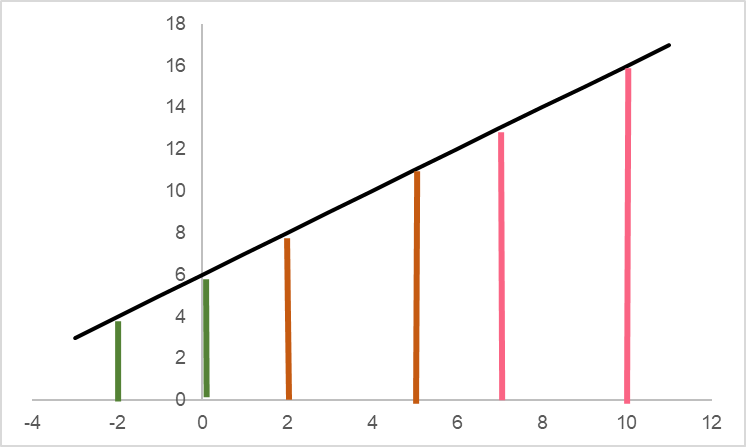
To get the area between an interval, you simply need to take the area of the upper limit minus the area of the lower limit.
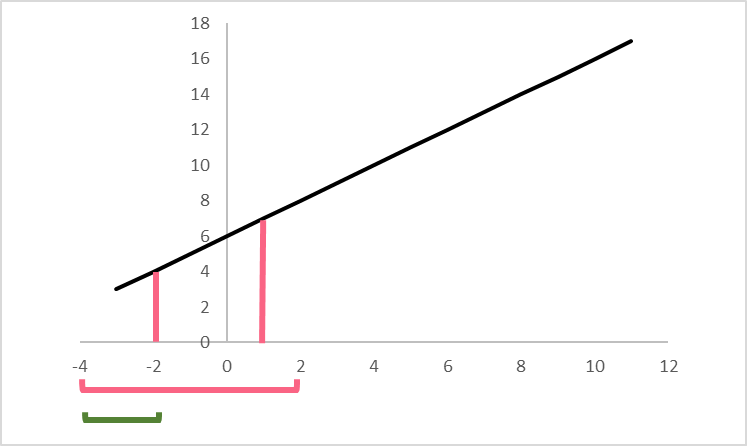
| Step 1 | Find the integral of 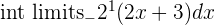 | 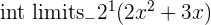 |
| Step 2 | Get the area of the upper limit |  = 5 = 5 |
| Step 3 | Get the area of the lower limit |  = 2 = 2 |
| Step 4 | Get the area between the limits | 5-2 = 3 |
Integration Rules
You can think of integration as the opposite as taking the derivative. Let’s compare each by seeing the rule for taking the integral and derivative or a power.

| Start with a power function | f =  |
| Take the derivative | f’ = 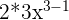 = = 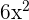 |
| Take the integral of the derivative | 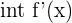 = = 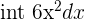 = =  = = 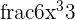 = =  |
In the table above, we can see that by taking the integral of the derivative, we have come back to the original function. Take a look at more integration rules and examples below.
| Integral Function | Result | Example | |
| Constant |  | 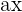 | 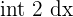 = 2x + c = 2x + c |
| Power | 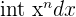 | 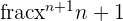 | 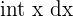 = = 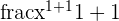 = = 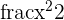 |
| Fraction of x | 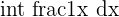 | 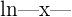 | 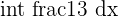 = =  |
| Natural Log | 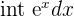 | 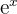 | 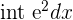 = = 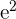 |
| Exponential | 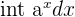 |  | 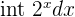 = = 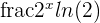 |
| Log |  | 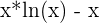 | 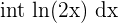 = =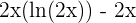 |
| Sum of two functions |  |  + +  | 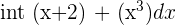 = =  + + 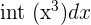 |
| Two functions subtracted |  |  - -  |  = =  - - 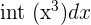 |
Integration by Parts
When you have two functions multiplied by each other, you can use integration by parts. The rule is as follows:
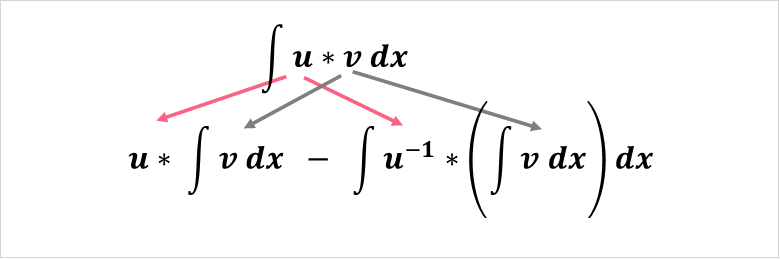
| Element | Description |
| u(x), u | The first function |
| v(x), v | The second function |
| u’(x), u’ | The derivative of the first function |
Say you have the following function to integrate:

We can use the rule in order to find the integral.
| Element | Description | Result |
| u(x), u | The first function | x |
| v(x), v | The second function | 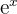 |
| u’(x), u’ | The derivative of the first function | 1 |
Plugging this into the rule, we get:

Now we solve for each term:
| A |  |
| B | 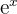 |
| C | 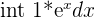 = = 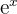 |
The final result is:
[
x*e^{x} - e^{x}
]
Integration by Substitution
Also called u-substitution, Integration by substitution can be used if you have two functions, one of which can be written as the derivative of the first function.

The goal is to simplify the integration process. So, we can pick the inside function as our ‘u.’
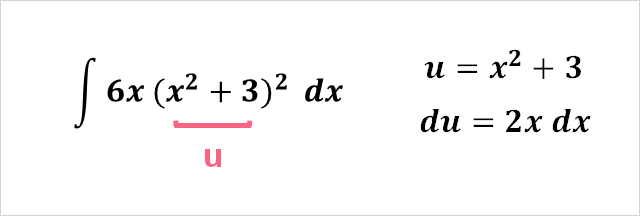
Now that we selected a u and have attained the derivative, what we need to do now is get the dx term by itself.

Now, we simply replace the function that we’ve chosen as our u by the u term and replace the dx term with what we just solved.

Now, we simplify.

Recall that a function multiplied by a constant in an integral is just that constant multiplied by the integral.

Now, instead of the complicated formula we had in the beginning, we can solve the integral easily.

The final step is to simply substitute the ‘u’ back into the equation.

Problem 1
Integrate the following function using any of the rules above:
[
int 3(x+1)^{2} dx
]
Problem 2
Integrate the following function using any of the rules above:
[
int limits_2^5 (4x + x)^{2} dx
]
Problem 3
Integrate the following functions using integration by parts:
[
int 4x(x+2)^{3} dx
]
Problem 4
Integrate the following function using u-substitution.
[
int x^{4}e^{x^{5}} dx
]
Problem 5
Integrate the following functions using any of the rules above:
[
int 2x(x+1)^{3} - 12x(sqrt{10 - 2x^{2}})dx
]
Solution Problem 1
Let’s integrate this function using u-substitution:
[
int 3(x+1)^{2} dx
]
[
u = x+1
]
[
du = 1 dx
]
[
int 3u^{2} du = 3(frac{u^{2+1}}{2+1})
]
[
int 3u^{2} du = 3(frac{(x+1)^{3}}{3})
]
Solution Problem 2
Let’s integrate the function:
[
int limits_2^5 (4x + x)^{2} dx = int limits_2^5 (5x)^{2} dx = int limits_2^5 25x^{2} dx
]
[
25 * int limits_2^5 frac{x^{3}}{3}}
]
[
25*(frac{5^{3}}{3}} - frac{2^{3}}{3}}) = 975
]
Solution Problem 3
For this function we use integration by parts:
[
int 4x(x+2)^{3} dx
]
The integration of 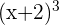 is exactly the same as in problem 1.
is exactly the same as in problem 1.
[
4x * (frac{(x+1)^{4}}{4}) - int (4 * ((x+1)^{4}*frac{1}{4})) dx
]
Let’s focus on the second term.
[
4*frac{1}{4} int ((x+1)^{4}) dx
]
The integration of 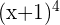 is the same as problem 1.
is the same as problem 1.
[
4x * (frac{(x+1)^{4}}{4}) - (frac{(x+1)^{5}}{5})
]
Solution Problem 4
First, you need to pick which function will be your u term.

Next, take the derivative and solve for dx.

Plug everything back into the equation and simplify.

Lastly, plug the u term back in.

Solution Problem 5
In this integral, you first need to use the difference rule.

Use integration by parts for the first integral.
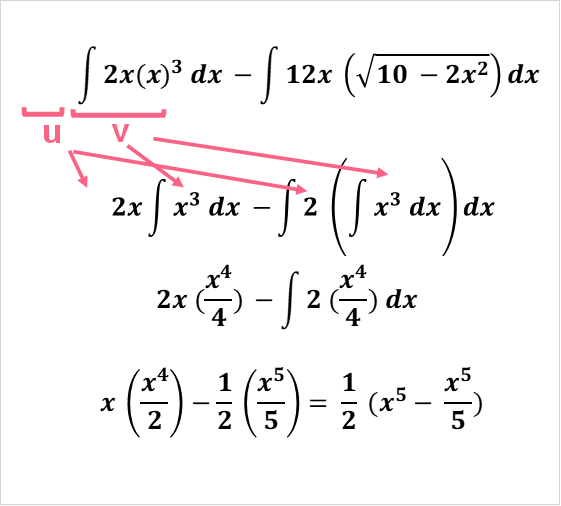
Use u-substitution for the second integral.

Finally, put it all together.














Hi,
what is the integral of ;
(k ^ -u x e ^ u)
Thanks,