Chapters

Integration
Integration is an important concept of calculus. When you integrate an equation, you are simply finding the area beneath that equation’s graph. To understand better, take a linear equation:
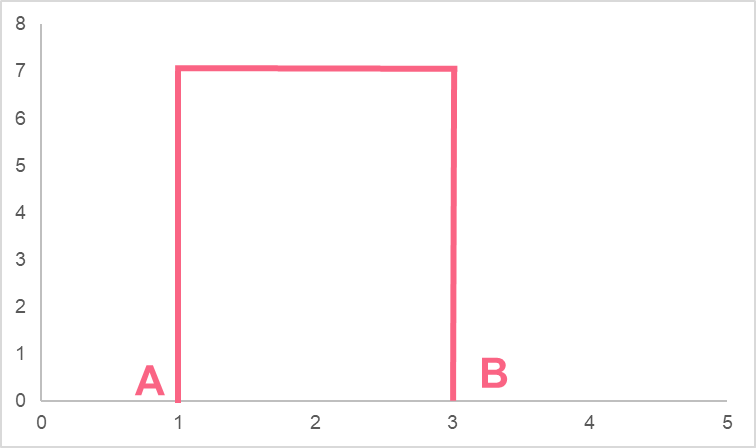
We can easily find the area beneath this line by finding the distance between the line and the axis, or even by simply counting the squares underneath it. Take a look at another example:
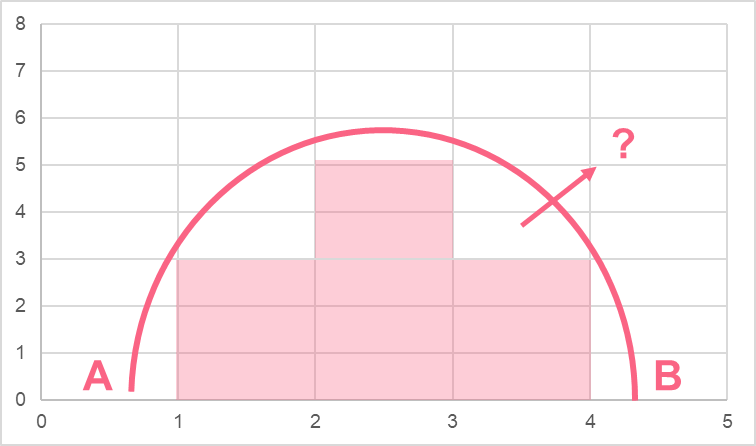
While we can count the area with whole squares, how can we measure the other squares? Do we take only half, or a third? This is where integration comes in:
Integration Notation
When we’re interested in integrating a function, this is also known as the reverse of the derivative.
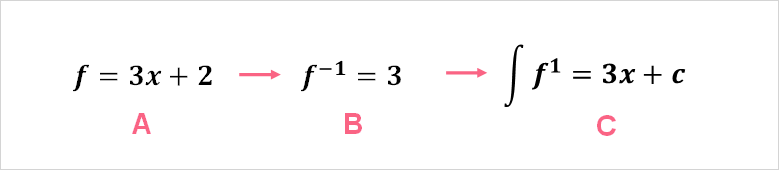
| A | B | C |
| Function | First derivative of the function | Integral of the function |
Take a look at the notation of integration:
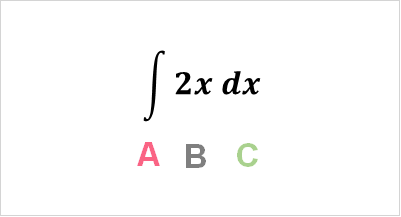
| A | Integration symbol |
| B | Function |
| C | This tells you which variable to integrate |
An integral can be either definite or indefinite.

| B | A |
| Definite | Indefinite |
| The area between a defined interval | The area of the entire function |
You will mostly encounter definite intervals.
Constants
Constants are the easiest to integrate. The rule for integrating constants can be found in the table below.
| Integral | Rule | Example | |
| Constant |  | ax + c |  = 4x + c = 4x + c |
The reason why we put a constant c is because the derivative of any constant is zero.
| Function | Derivative | Integral |
| 4x + 30 | f’ = 4x + 0 | 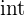 4x dx = 4x + c 4x dx = 4x + c |
| 4x + 2 | f’ = 4x + 0 | 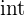 4x dx = 4x + c 4x dx = 4x + c |
| 4x | f’ = 4x | 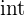 4x dx = 4x + c 4x dx = 4x + c |
Adding the constant c to the integral reflects the fact that there might have been a constant in the original function.
Let’s take the following as an example:

To find the area, we simply subtract the upper interval and the lower interval.

Exponents
Integrating exponents follows a similar process as above. Take a look at the exponent rule below.

This rule should be applied to every exponent you want to integrate. Let’s take a look at an example.

The table below has the steps for integrating this exponent.
| Step 1 | Follow the rule specified above |  |
| Step 2 | Simplify the fraction |  |
Fractions
To integrate fractions, you will need a mix of the exponent rule as well as the following rules.
| Power/Fraction Rule | 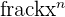 | =  |
| Reciprocal Integral Rule | 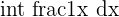 | = ln|x| |
| Integration by Parts | 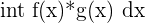 | = 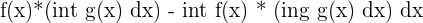 |
| U-substitution Integration | 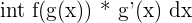 | = 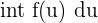 |
Let’s take one example and integrate it two ways. First, let’s rewrite the function using the power/fraction rule.

| Step 1 | Rewrite the function | 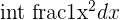 = = 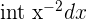 |
| Step 2 | Integrate using the exponent rule | 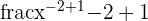 |
| Step 3 | Simplify |  = =  |
Next, we can use u-substitution and the exponent rules. First, we write down our parameters.
| u | 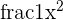 = =  |
| du |  |
| dx | 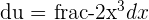
|
| x |  x^{-2} x^{-2} sqrt{x} = sqrt{frac{1}{u}} sqrt{x} = sqrt{frac{1}{u}} x = sqrt{frac{1}{u}} = (u^{-1})^{frac{1}{2}} x = sqrt{frac{1}{u}} = (u^{-1})^{frac{1}{2}} x = u^{frac{1}{2}} x = u^{frac{1}{2}} |
Next, we replace the function with our parameters above.

We also have to replace the x in our function.

Simplify the u terms.

Now, integrate the function.

Exponential and Logarithms
In order to integrate exponential or logarithmic function, you will need to follow the rules for integration.
Exponential Function
Recall that an exponential function is one that has the variable in the exponent. Take a look at the notation and an example below.
| Notation | Example |
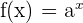 |  |
In order to integrate this function, we need to follow the following rule.
| Integral Exponential | Integral Rule | Example |
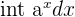 |  |  |
Euler's number
Euler's has a fixed value, which is e approximately equal to 2.718. Take a look at the notation and an example below.
| Notation | Example |
 | 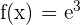 |
In order to integrate this function, we need to follow the following rule.
| Integral Euler's | Integral Rule | Example |
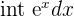 | 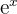 | 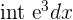 = |
Natural Logarithm
Natural logarithms have Euler’s number as the base. Take a look at the notation and an example below.
| Notation | Example |
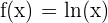 |  |
In order to integrate this function, we need to follow the following rule.
| Integral Natural Log | Integral Rule | Example |
 |  | 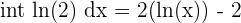 |
Sum Rule
When you have to integrate the sum of two functions, you simply integrate each function separately.
| Integral Function | Rule |
 | 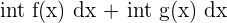 |
Difference Rule
When you have to integrate the difference of two functions, it is the same as when you have the sum of two functions.
| Integral Function | Rule |
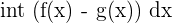 | 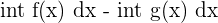 |













Hi,
what is the integral of ;
(k ^ -u x e ^ u)
Thanks,