Chapters

Polynomial Function
| Type | Definition | Example | |
| A | Monomial | One monomial | Constant |
| B | Binomial | Two monomials | Linear function |
| C | Trinomial | Three monomials | Quadratic function |
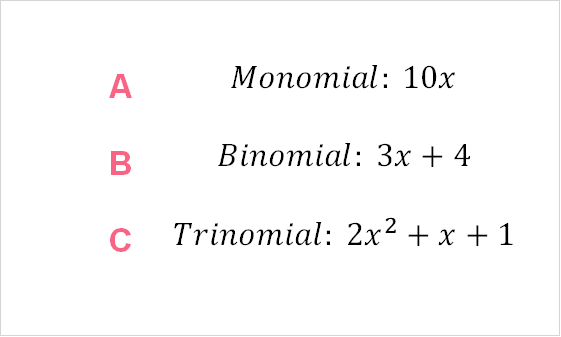
Rational Function
A rational function is defined as a function that divides one polynomial by another. This is easy to remember because of the word rational.

Above, you can see that a rational function is simply the ratio of two polynomial functions. Keep in mind that even regular polynomials can be rational functions.
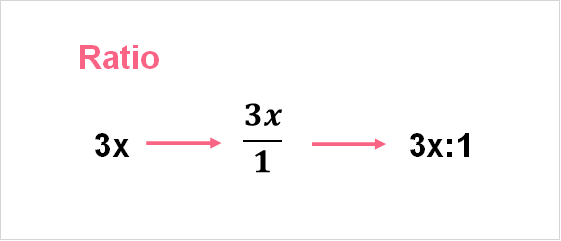
By dividing the polynomial by 1, we get a ratio of any polynomial function and a monomial. A rational function can be simple, like in the examples above, or more complex. The table below has some examples of more complex rational functions.
| Example | Numerator | Denominator |
 | Linear | Quadratic |
 | Square root of linear | Linear |
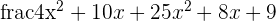 | Quadratic | Quadratic |
Rational Function Simplification
Whenever you’re dealing with rational functions, the first thing you have to do is simplify them. Let’s look at an easy example first.

Whether we’re graphing this rational function or integrating it, we should always try to simplify it. This will make it easier to perform any operation on it afterwards. The simplification steps for this rational function are in the table below.
| Description | Problem | |
| Step 1 | See if the numerator and denominator have common terms | There is an x term in both |
| Step 2 | Split up the numerator |  |
| Step 3 | Cancel out any terms that are alike | 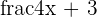 |
Here are some more tips you can use to simplify any rational function.
| Example | |
| See if the numerator or denominator have any like terms |  |
| Test whether the numerator or denominator can be simplified by themselves | 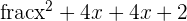 = =  |
| Add like terms | 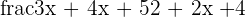 = =  |
Integration
Integration is one of the most important concepts in calculus. You can think about integration in two ways:
| 1 | Integration is the opposite of taking the derivative |  |
| 2 | Integrating a function gives us the equation for the area |  |
Notice that the notation is the same for both points of view. Whether you think about it in the first or second way, the process of integration is always the same. You may also see the notation like this:
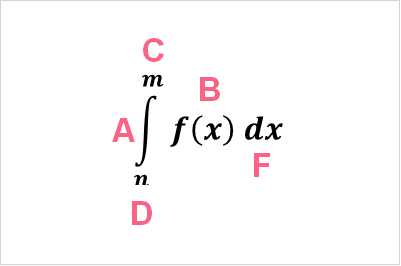
| A | Integral sign | The sign for integration |
| B | Function | The function we want to integrate |
| C | Lower bound | The lower limit of the interval we want to find the area for |
| D | Upper bound | The upper limit of the interval we want to find the area for |
| E | dx | Specifies the variable to integrate |
Integration of a Fraction
There are several ways you can integrate a fraction. First, take a look at some basic integration rules.
| Integration Function | Result | |
| Constant |  | 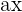 |
| Power | 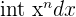 | 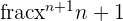 |
| Reciprocal | 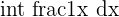 | 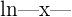 |
Take a look at some examples below.
| Integration | Result | |
| Constant | 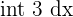 |  |
| Power | 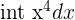 | 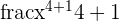 = = 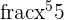 |
| Reciprocal |  | 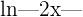 |
This means that, depending on what fraction you have, you can integrate several ways. The first method is to use the following rule.

Let’s take the following fraction as an example.

To make this function easier to integrate, we can use the rules of powers to get the following:

The second method is to use the reciprocal rule. In many instances, we can combine this with u-substitution:

Integration of Rational Function
Integrating rational function requires using all the techniques mentioned above. You may encounter more complex functions, which have the following rules:
| Integration Function | Result | |
| Log |  | 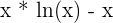 |
| Cosine |  | sin(x) |
| Sine |  | -cos(x) |
| Tangent |  | tan(x) |
Take a look at some examples below.
| Example | Result | |
| Log | 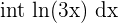 |  |
| Cosine | 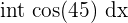 | sin(45) |
| Sine |  | -cos(20) |
Since rational functions are fractions, we can use power rules like in the examples before. However, you will also need u-substitution and integration by parts.
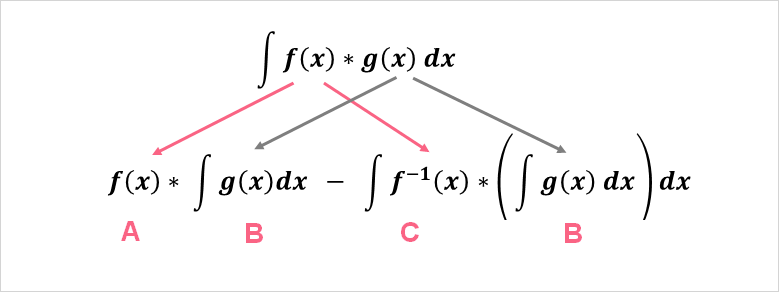
Where:
| A | Function f(x) |
| B | Function g(x) |
| C | Derivative of f(x) |
Let’s take an example.

Using integration by parts, we do the following:

Now, we simply follow the integration rules.

Now, we simplify.

Example 1
Let’s do a step-by-step integration of a rational function. Take the function below as an example.
[
int x^{3} dx
]
Here, we can simply use the power integration rule. First, use the rule to find the result.
[
int x^{3} dx = frac{x^{3+1}}{3+1}
]
Next, simplify the equation to get the final result.
[
frac{x^{3+1}}{3+1} = frac{x^{4}}{4}
]
Example 2
In the last example, you worked with an indefinite integral. Let’s take the same example, but work with a definite integral instead.
[
int limits_3^5 x^{3} dx
]
We work with the results from the previous example.
[
int limits_3^5 frac{x^{4}}{4} = frac{5^{4}}{4} - frac{3^{4}}{4} = 136
]
Example 3
Let’s work with u-substitution in this example. You have the following integral.
[
int sqrt{3x + 1} dx
]
Let’s substitute 3x+1 with u. So, let’s find the derivative of the u term.
[
du = 3 dx
]
Solve for the dx term.
[
dx = frac{du}{3} = frac{1}{3}*du
]
Replace these terms into the original integral.
[
int sqrt{u} du frac{1}{3}
]
Simplify this integral.
[
frac{1}{3} int u^{frac{1}{2}} du
]
Solve using the power rule.
[
frac{1}{3} (frac{u^{frac{3}{2}}}{frac{3}{2}})
]
Plug u term back in.
[
frac{1}{3} (frac{(3x+1)^{frac{3}{2}}}{frac{3}{2}})
]













Hi,
what is the integral of ;
(k ^ -u x e ^ u)
Thanks,