Chapters
In this article, we will discuss how to find integrals of trigonometric functions with examples. But before proceeding to the examples, first, let us see what is meant by integration.

What is Integration?
"An integration refers to computing the integral of a given function"
In mathematics, integrals help us to calculate certain useful quantities such as volumes, area, and displacement, etc. When we say that we are finding an integral of the function, then it means that we are calculating the definite integral of the function. We use indefinite integrals for anti-derivates of the function. Integration and differentiation are the two major concepts in calculus.
The integration represents the summation of the discrete data. In other words, we can say that we use integration to calculate functions that cannot be calculated individually because they are composed of small pieces of data. Examples of these functions include area, volume, displacement. Finding integrals is the basis of integral calculus and it helps to solve the following types of problems:
- Finding the problem function, given the derivatives of a function
- Finding area covered by the function's graph under certain constraints
The fundamental theorem of calculus is used to associate the concepts of differentiating and integrating a function. In the next section, we will discuss what are trigonometric integrals.
Trigonometric Integrals
The integrals of trigonometric functions are known as trigonometric integrals. The integrals of the common trigonometric functions are given below:
1.  cos x dx = sin x + C
cos x dx = sin x + C
2.  sin x dx = -cos x + C
sin x dx = -cos x + C
3.  x dx = tan x + C
x dx = tan x + C
4. 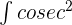 x dx = - cotanx + C
x dx = - cotanx + C
5.  (sec x tan x)dx = sec x + C
(sec x tan x)dx = sec x + C
6.  (cosec x cotan x)dx = - cosec x + C
(cosec x cotan x)dx = - cosec x + C
Strategies Used for Integrating the Trigonometric Functions
In this section, we will see what strategies one should use while integrating the function of the form 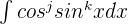 .
.
- If k is an odd number, then rewrite
 as
as 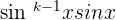 . Then, use the identity rule
. Then, use the identity rule 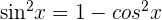 for rewriting
for rewriting  in terms of cos x. In the next step, integrate the function by substituting cos x = u. This substitution gives the value of du = -sin x dx.
in terms of cos x. In the next step, integrate the function by substituting cos x = u. This substitution gives the value of du = -sin x dx.
- If j is an odd number, then rewrite
 as
as 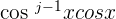 . Then, use the identity rule
. Then, use the identity rule 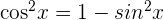 for rewriting
for rewriting 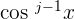 in terms of sin x. In the next step, start integrating the function by substituting sin x = u. This substitution gives the value of du = cos x dx.
in terms of sin x. In the next step, start integrating the function by substituting sin x = u. This substitution gives the value of du = cos x dx.
- If both j and k are odd numbers, then you can use either the first or the second strategy.
- If both j and k are even numbers, then use
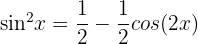 , and
, and 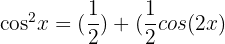 . When you have applied these formulas, then you can integrate the function by applying the above strategies where necessary.
. When you have applied these formulas, then you can integrate the function by applying the above strategies where necessary.
Now, we will solve some examples in which we will find the integrals of the trigonometric functions.
Example 1
Compute the integral of the following function:
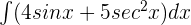
Solution
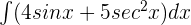 can be written as:
can be written as:

According to one of the properties of integrals, the constants can be moved before the integral sign. Hence, we can write the above function as:

We know that  sin x dx = -cos x + C and
sin x dx = -cos x + C and  x dx = tan x + C. Hence, we can substitute these values in the above function to get the final answer:
x dx = tan x + C. Hence, we can substitute these values in the above function to get the final answer:
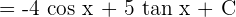
Example 2
Compute the integral of the following function:
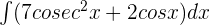
Solution
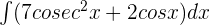 can be written as:
can be written as:
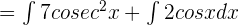
According to one of the properties of integrals, the constants can be moved before the integral sign. Hence, we can write the above function as:

We know that  cosec^2 x dx = - cotan x + C and
cosec^2 x dx = - cotan x + C and  x dx = sin x + C. Hence, we can substitute these values in the above function to get the final answer:
x dx = sin x + C. Hence, we can substitute these values in the above function to get the final answer:
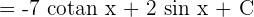
Example 3
Calculate the integral of the following function:
 cos (3x + 2) dx
cos (3x + 2) dx
Solution
In this example, we will use substitution to calculate the integral. Suppose 3x + 2 = u.
If u = 3x + 2, then 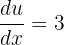 . This means that
. This means that 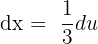 . Substituting these values in the original function will give us the following function:
. Substituting these values in the original function will give us the following function:
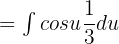
Move the fraction before the integral sign:
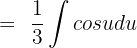
We know that  cos x dx = sin x + C. Hence, we will substitute this value in the above function:
cos x dx = sin x + C. Hence, we will substitute this value in the above function:
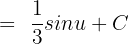
Since u = 3x + 2, hence substitute this value of u in the above function again:
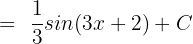
Example 4
Calculate the integral of the following function:
 sin (8x - 5) dx
sin (8x - 5) dx
Solution
In this example, we will use substitution to calculate the integral. Suppose 8x - 5 = u.
If u = 8x - 5, then 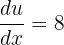 . This means that
. This means that 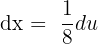 . Substituting these values in the original function will give us the following function:
. Substituting these values in the original function will give us the following function:
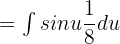
Move the fraction before the integral sign:
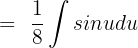
We know that  sin x dx = -cos x + C. Hence, we will substitute this value in the above function:
sin x dx = -cos x + C. Hence, we will substitute this value in the above function:
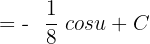
Since u = 8x - 5, hence substitute this value of u in the above function again:
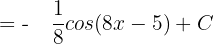
Example 5
Calculate the integral of the following function:
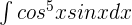
Solution
We will solve this example through substitution. Suppose 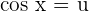 . Then
. Then 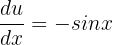 . This shows that
. This shows that 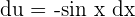 . Substitute these values in the original function like this:
. Substitute these values in the original function like this:
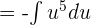
We know that the integral of 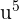 is equal to
is equal to 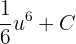 . Hence, we substitute this value in the above function like this:
. Hence, we substitute this value in the above function like this:
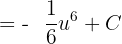
Substitute the value of u again in the above function:
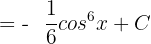
Example 6
Evaluate the following function:
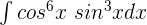
Solution
You can see that the power of sin x is odd, hence we can write the above function using strategy 1 like this:

Substitute 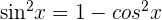 in the above function:
in the above function:

Suppose u = cos x, then du = -sin x:
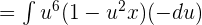

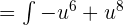
Integrate the above function like this:
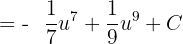
Substitute u = cos x again in the above function:
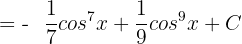












Hi,
what is the integral of ;
(k ^ -u x e ^ u)
Thanks,