Chapters

What is Integration?
Integration is an operation which helps you determine the area under the graph of a function.

| A | B | C | |
| Integral | Integral sign | Function | Tells us which variable we’re integrating |
| Example | 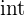 | 2b + 4 | db |
Notice that we don’t always have to use ‘dx,’ as this part of an integration formula will depend on which variable we’re integrating.
When we plot the example from the table above, the integration of this function can give us the area underneath it.
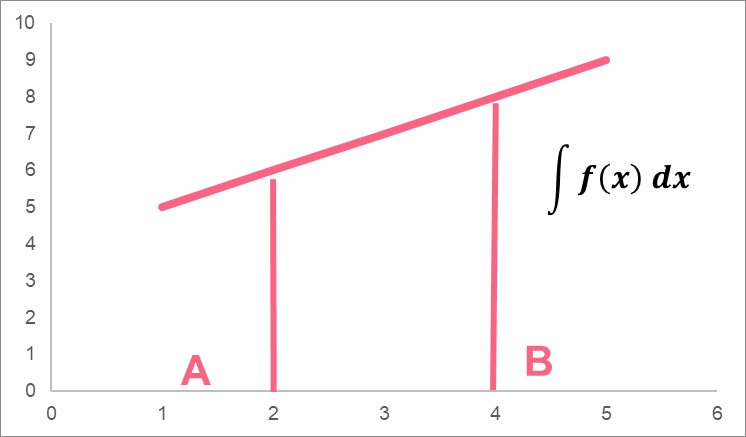
Indefinite Integral
An indefinite integral is an integral whose bounds are limited to the graph of the function.

| A | B | C | |
| Integral | Integral sign which has no upper or lower bound | Function | Tells us which variable we’re integrating |
As you can see, an indefinite integral has no upper or lower bound. This means that this integrated formula can give us the area under any point on the graph:
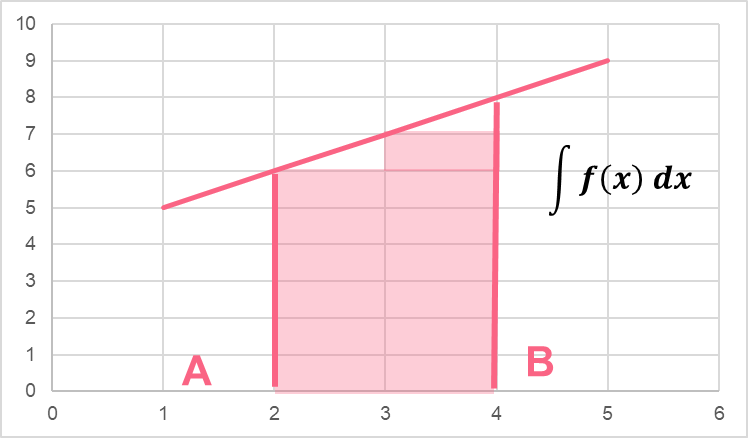
Definite Integral
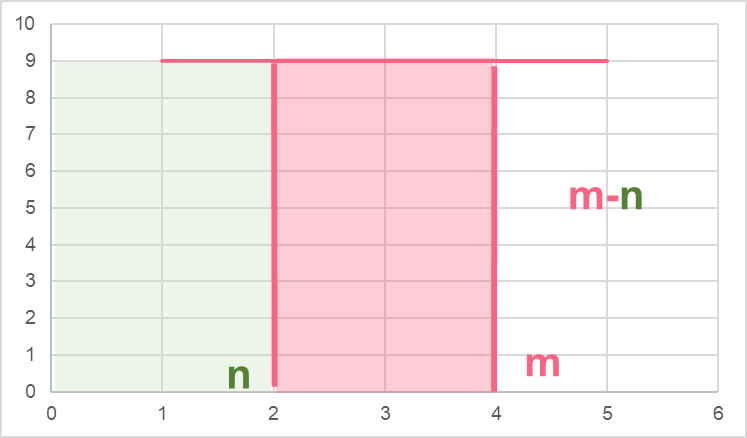
A definite integral has bounds that are defined in the integration equation.

| A | B | C | |
| Integral | Integral sign which has upper bound of m and lower bound of n | Function | Tells us which variable we’re integrating |
As you can see, the main difference between an indefinite and a definite integral is that a definite integral is defined by bounds of the interval [n,m].
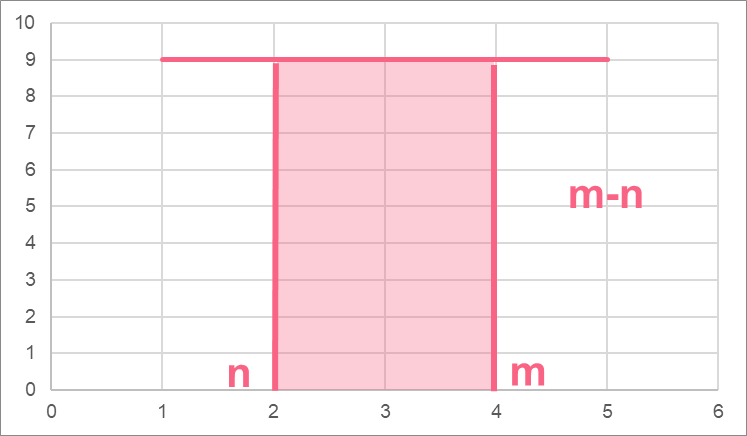
In order to get the area of the interval between n and m, we simply do the following:
| Step 1 | Integrate the function | 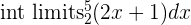 = = 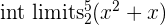 |
| Step 2 | Plug in m to the integrated equation |  = 30 = 30 |
| Step 3 | Plug n to the integrated equation |  = 6 = 6 |
| Step 4 | Get m - n | 30 - 6 = 24 |
Integration Rules
Now that you know the logic behind what integration is and why we use it, take a look at integration rules.
Constant
| Integral Function | Rule | |
| Constant |  | ax |
Here are some examples:
| Integral Function | Result | |
| 1 |  | 4x + c |
| 2 | 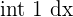 | x + c |
| 3 | 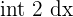 | 2x + c |
Integration can be thought of doing the opposite of finding the derivative. Take a look at the example below.
| Function | Derivative | Integral |
| 4x + 2 |  |  = =  |
| f = 4x + 2 | f’ =4 | 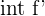 = 4s + c = 4s + c |
We can never get the exact constant of the original formula, but we can put ‘c’ there to stand in for the constant that was there.
Fraction
There are two ways you can integrate a fraction. First, convert the fraction into a regular number.

Instead of integrating the fraction, we can use common exponent rules to turn it into two numbers multiplied by each other.

Another way you can integrate a fraction is to see if it follows the rule for integrating reciprocals.

You can combine any of the methods we discussed, as well as use them with integration by parts and u-substitution.
Sum
The sum rule of integration is a simple rule. It says that if you have to integrate the sum of two functions, the result is equal to the integration of both functions added together.

| What | Example | |
| f(x) | First function | x+3 |
| g(x) | Second function | 5x |
Let’s take a look at an example.

First, we simplify the expression.

Next, because it is the addition of two functions, we can integrate them separately.

Difference
The difference rule of integration is similar to the sum rule. It says that if you have to integrate the difference of two functions, the result is equal to the integration of one function minus the other.

| What | Example | |
| f(x) | First function | 2x |
| g(x) | Second function (that we subtract from the first) | 4x+3 |
Let’s take a look at an example.

First, we simplify the expression.

Next, because it is the difference of two functions, we can integrate them separately.

Power
Powers are a very important part of integration. The rule is as follows.

| x | The variable we’re integrating |
| n | The exponent, or power |
What about when you don’t have any power? Take a look at this example.

Well, in this case, the power is actually there. It is equal to one, because a number to the power of 1 is just itself. So, it would be the following.

Integration by Parts
Integration by parts is exactly as it sounds. When you have two functions multiplied together, you can use integration by parts to integrate them.
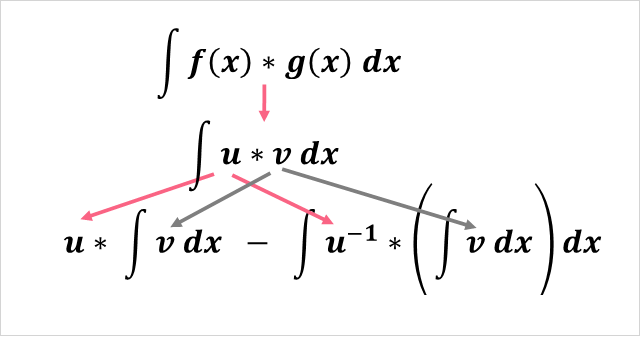
| What | Example | |
| u | The first function | 3x |
| v | The second function | 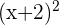 |
| u’ | The derivative of the first function | 3 |
Keep in mind, however, that you should only integrate by parts if you have two functions that will not produce more functions that need to be integrated by parts. To understand this, let’s take an example that we actually can use this method for.

Now, we follow the rule.

Simplifying only the highlighted term, we get the following.

Now, imagine if we didn’t have this term, but instead had this.
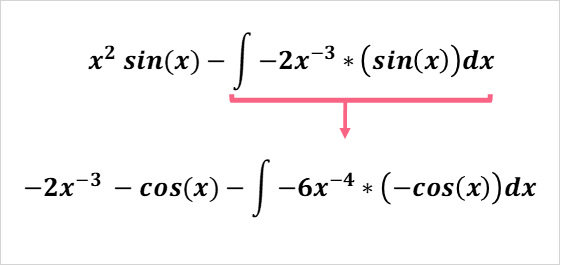
When we simplify this term, we end up with another two functions multiplied by one another. This means that we would need to keep integrating by parts infinitely. If you end up with this, it is better to integrate by u-substitution.
Integration by Substitution
Integration by substitution, also called u-substitution, is an easy way to integrate. Let’s take a look at the notation and a simple example.

| u | The expression we want to replace | 4x |
| du | The derivative of the expression | 4 dx |
| dx | Solve for dx | 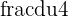 |
Continuing with our example from above, let’s take a look at the steps in u-substitution.
| 1 | Replace the u and dx values in the formula |  = =
|
| 2 | Simplify the expression |  = =
|
| 3 | Integrate like normal |  |
| 4 | Simplify | 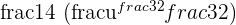 |
| 5 | Plug the original value of u back in to get the final result |  = |










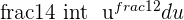



Hi,
what is the integral of ;
(k ^ -u x e ^ u)
Thanks,