Chapters
In this article, we will discuss how to calculate the area between a function and the x-axis.

Area between a Function and the x-axis
There are two scenarios in which we can find the area between a function and the x-axis:
- When the function is non-negative, i.e. positive
- When the function is negative
Now, let us see what steps one should follow while calculating the area between the function and x-axis.
Steps for Calculating Area Under the Curve
To compute the area under the curve f(x), one should follow the steps below:
Step 1 - Sketch the area
Step 2 - Find the boundaries a and b
Step 3 - Write the definite integral function
Step 4 - Integrate the function
In the next section, we will discuss how to calculate the area when the function is positive.
When the Function is Positive
If the function f(x) is positive on an interval [a, b], then the area of the region bounded by the graph of the function f, the horizontal axis (x - axis) and the vertical lines x = a, and x = b is defined as follows:
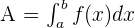
Now, let us solve some examples in which we will calculate the area under the curve.
Example 1
Calculate the area bounded by the function  and the x-axis.
and the x-axis.
Solution
Follow these steps to solve this example.
Step 1 - Sketch the graph
Sketch the graph. The graph of the function  is given below:
is given below:

Step 2 - Find the boundaries
To find the boundaries a and b of the function, we have to determine the x-intercepts of the curve. Although, from the graph above, we can clearly determine that the limits of integration are 3 and -3, however, we can check it again by equating the function  equal to zero as shown below:
equal to zero as shown below:
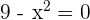
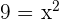

Step 3 - Using the boundaries, write the definite integral function
In this step, we will use the boundaries 3 and -3 and write the function in definite integral form like this:
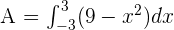
Step 4 - Integrate the function
Write the function 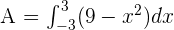 using the sum/difference property of definite integrals like this:
using the sum/difference property of definite integrals like this:
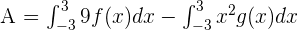
Now, to find the definite integral of the function, first, we will calculate the antiderivative of the function. The antiderivative of the function is 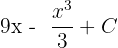 . For ease of calculation, consider C = 0.
. For ease of calculation, consider C = 0.
The fundamental theorem of calculus says that:
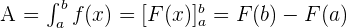
Substitute 3 and -3 in the antiderivative of the function:
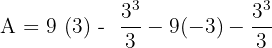
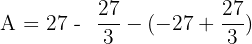
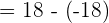
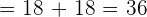
Hence, the area bounded by the function  and the x- axis is
and the x- axis is 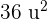
Example 2
Calculate the area of the region enclosed by the function xy = 36, the lines x = 6 and x = 12 and the x-axis.
Solution
Follow these steps to compute the area.
Step 1 - Sketch the graph
The graph of the function 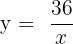 is given below:
is given below:
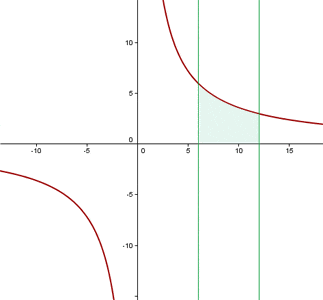
Step 2 - Find the boundaries
The boundaries x = 6 and x = 12 are already given in this problem.
Step 3 - Using the boundaries, write the definite integral function
In this step, we will use the boundaries 6 and 12 and write the function in definite integral form like this:
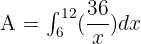
Step 4 - Integrate the function
Now, to find the definite integral of the function, first, we will compute the antiderivative of the function. The antiderivative of the function is 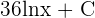 . For ease of calculation, consider C = 0.
. For ease of calculation, consider C = 0.
The fundamental theorem of calculus says that:
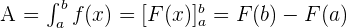
Substitute 6 and 12 in the antiderivative of the function like this:
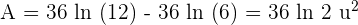
When the Function is Negative
If the function is negative in a closed interval [a, b] then the graph of the function is below the horizontal axis. The area of the function can be defined like this:
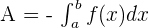

Now, let us solve some examples in which we are given a negative function.
Example 1
Find the area of the function bounded by the graph of  and x-axis.
and x-axis.
Solution
Follow these steps to solve this example.
Step 1 - Sketch the graph
Sketch the graph. The graph of the function  is given below:
is given below:
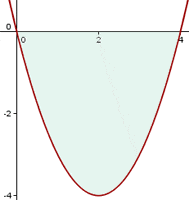
The downward parabola shows that the function is negative.
Step 2 - Find the boundaries
To find the boundaries a and b of the function, we have to determine the x-intercepts of the curve. Although, from the graph above, we can clearly determine that the limits of integration are 4 and 0, however, we can check it again by equating the function  equal to zero as shown below:
equal to zero as shown below:
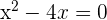
 or
or 
Step 3 - Using the boundaries, write the definite integral function
In this step, we will use the boundaries 4 and 0 and write the function in definite integral form like this:

Step 4 - Integrate the function
Write the function  using the sum/difference property of definite integrals like this:
using the sum/difference property of definite integrals like this:
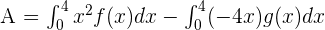
Now, to find the definite integral of the function, first, we will calculate the antiderivative of the function. The antiderivative of the function is 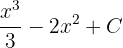 . For ease of calculation, consider C = 0.
. For ease of calculation, consider C = 0.
The fundamental theorem of calculus says that:
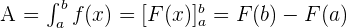
Substitute 4 and 0 in the antiderivative of the function:
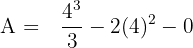

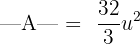
Example 2
Calculate the area bounded by the curve y = cos x and the x-axis between  and
and 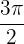 .
.
Solution
Follow these steps to solve this example.
Step 1 - Sketch the graph
Sketch the graph. The graph of the function y = cos x is given below:
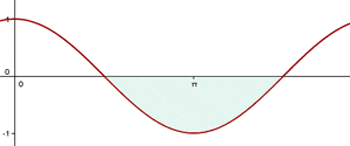
Step 2 - Find the boundaries
The boundaries 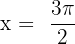 and
and 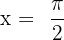 are already given in this problem.
are already given in this problem.
Step 3 - Using the boundaries, write the definite integral function
In this step, we will use the boundaries 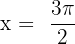 and
and 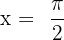 to write the function in definite integral form like this:
to write the function in definite integral form like this:
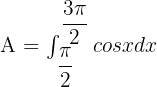
Step 4 - Integrate the function
Now, to find the definite integral of the function, first, we will compute the antiderivative of the function. The antiderivative of the function is 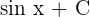 . For ease of calculation, consider C = 0.
. For ease of calculation, consider C = 0.
The fundamental theorem of calculus says that:
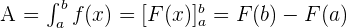
Substitute 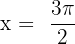 and
and 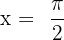 in the antiderivative of the function like this:
in the antiderivative of the function like this:
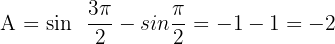
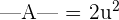













Hi,
what is the integral of ;
(k ^ -u x e ^ u)
Thanks,