Chapters
In this resource, you will find solved examples of triginometric examples. Before proceeding to examples and their solutions, first, let us see the anti derivatives of the common trigonometric functions.

Common Trigonometric Integrals
The integrals of trigonometric functions are referred to as trigonometric integrals. The integrals of the common trigonometric functions are compiled below:
1.  cos x dx = sin x + C
cos x dx = sin x + C
2.  sin x dx = -cos x + C
sin x dx = -cos x + C
3.  x dx = tan x + C
x dx = tan x + C
4. 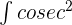 x dx = - cotanx + C
x dx = - cotanx + C
5.  (sec x tan x)dx = sec x + C
(sec x tan x)dx = sec x + C
6.  (cosec x cotan x)dx = - cosec x + C
(cosec x cotan x)dx = - cosec x + C
The above list is quite helpful in solving the problems related to trigonometric integrals.
Example 1
Calculate the following integral:

First, use the sum/difference property of integration to write the above function like this:
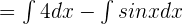
Compute the integrals of both the terms separately. The integral of 4 is 4x and the integral of sin x is cos x:
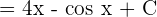
Example 2
Calculate the following integral:

Solution
Using the sum/difference property of integration, we can write the above function as:
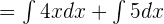
Calculate the integral or antiderivative of the two terms separately. The antiderivative of 4x is equal to 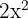 and the antiderivative of 5 is equal to 5x:
and the antiderivative of 5 is equal to 5x:
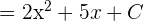
E
Example 3
Compute the antiderivative of the following function:

Solution
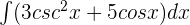 can be written as:
can be written as:

According to one of the properties of integrals, we can shift constants before the integral sign. Hence, we can write the above function like this:
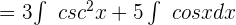
We know that  csc^2 x dx = - cotan x + C and
csc^2 x dx = - cotan x + C and  cos x dx = sin x + C. Hence, we will substitute these values in the above function like this:
cos x dx = sin x + C. Hence, we will substitute these values in the above function like this:
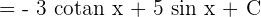
Example 4
Calculate the integral of the following function:
 sin (9x + 7) dx
sin (9x + 7) dx
Solution
In this problem, we will use substitution to compute the integral. Suppose 9x + 7 = u.
If u = 9x + 7, then 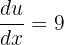 . This means that dx is equal to
. This means that dx is equal to 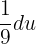 . Now, we will substitute these values in the original function to get the following function:
. Now, we will substitute these values in the original function to get the following function:
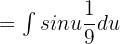
Shift the fraction before the integral sign:
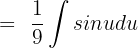
We know that  sin x dx = -cos x + C. Hence, we will substitute this value in the above function:
sin x dx = -cos x + C. Hence, we will substitute this value in the above function:
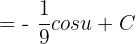
Since u = 9x + 7, hence we will substitute this value of u in the above function again to get the final answer:
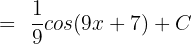
Example 5
Calculate the integral of the following function:
 cos (6x + 1) dx
cos (6x + 1) dx
Solution
In this problem, we will use substitution to compute the integral. Suppose 
If  , then
, then 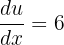 . This means that dx is equal to
. This means that dx is equal to 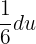 . Now, we will substitute these values in the original function to get the following function:
. Now, we will substitute these values in the original function to get the following function:
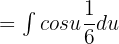
Shift the fraction before the integral sign:
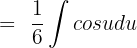
We know that  cos x dx = sin x + C. Hence, we will substitute this value in the above function:
cos x dx = sin x + C. Hence, we will substitute this value in the above function:
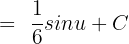
Since  , hence we will substitute this value of u in the above function again to get the final answer:
, hence we will substitute this value of u in the above function again to get the final answer:
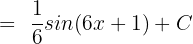
Example 6
Calculate the following integral:

Solution
Suppose 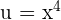 , then
, then 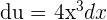 . It means that
. It means that 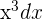 is equal to
is equal to 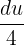 .
.
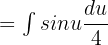
Shift fraction on the left side of the integral to get:
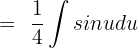
Remember that the antiderivative of sin u is equal to - cos u + C. Hence, we can write the function as:
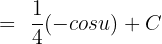
Put 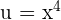 to get the following answer:
to get the following answer:
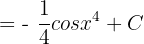
Example 7
Calculate the following integral:
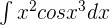
Solution
Suppose 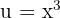 , then
, then 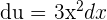 . It means that
. It means that 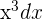 is equal to
is equal to 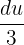 .
.
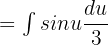
Shift fraction on the left side of the integral to get:
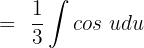
Remember that the antiderivative of cos u is equal to sin u + C. Hence, we can write the function as:
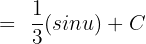
Put 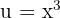 to get the following answer:
to get the following answer:
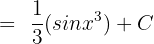
Example 8
Calculate the integral of the following function:
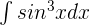
Solution
We can write  as the product of
as the product of 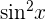 and sin x like this:
and sin x like this:

We know that  . This means that
. This means that 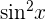 is equal to
is equal to  .
.
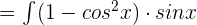
Substitute u = cos x:

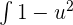 is equal to
is equal to 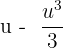 :
:
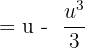
Substitute 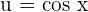 :
:
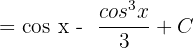
Example 9
Calculate the integral of the following function:
 tan (3x - 4) dx
tan (3x - 4) dx
Solution
In this problem, we will use substitution to compute the integral. Suppose 
If 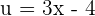 , then
, then 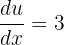 . This means that dx is equal to
. This means that dx is equal to  . Now, we will substitute these values in the original function to get the following function:
. Now, we will substitute these values in the original function to get the following function:
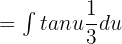
Shift the fraction before the integral sign:
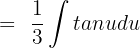
We know that  tan x dx = - ln |cos x| + C. Hence, we will substitute this value in the above function:
tan x dx = - ln |cos x| + C. Hence, we will substitute this value in the above function:
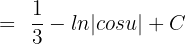
Since 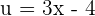 , hence we will substitute this value of u in the above function again to get the final answer:
, hence we will substitute this value of u in the above function again to get the final answer:
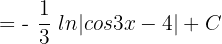
Example 10
Evaluate the following function:

Solution
As the power of sin x is odd, hence we can write the above function like this:
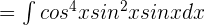
Substitute 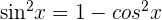 in the above function:
in the above function:

Suppose u = cos x, then du = -sin x:
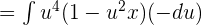
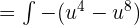

Integrate the above function like this:
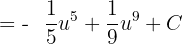
Substitute u = cos x again in the above function:
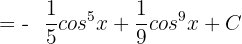













Hi,
what is the integral of ;
(k ^ -u x e ^ u)
Thanks,