Chapters
In this article, you will learn how to calculate the integral of power. But before proceeding to find the integral of power, first, let us see what are integrals.

What are Integrals?
The integrals of the functions are calculated using the process known as integration. In mathematics, integration is employed to compute the values of important quantities, for instance, area, volume, and displacement, etc. When we say that we are going to calculate the integral of a given function, then we actually mean that we will compute the definite integral of the function. The concept of integration helps us to find the problem function, given the derivatives of the function. It also helps us to calculate the area bounded by the graph of the function under some constraints.
The fundamental theorem of calculus links the differentiation and integration processes. Integration is in fact the inverse of differentiation. Finding the solutions of small addition problems is straightforward, which can be executed manually as well as with calculators. However, for bigger problems, the integration methods are used.
In the next section, we will see how to use the power rule of integration to find the integrals of functions involving powers or exponents.
Power Rule for Integrals
We can use the integral power rule to compute the integrals of a wide range of polynomials, root, and rational functions. The power rule formula for calculating the integrals of a power function is given below:
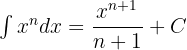
To use this rule, we simply take the exponent and add one to it. Then, we divide the expression with the same number. In the last step, we add the constant C.
Now, we will solve some examples in which we will find the integrals of the polynomials and root functions.
Example 1
Find 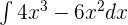
Solution
First, we will break down the integrals using addition/subtraction or multiplication by constants. Hence, we can write the above function like this:
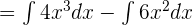
Now, we will shift the constants before the integral sign like this:

Now, we will apply the power rule 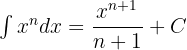 like this:
like this:
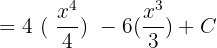
In the last step, write the final answer in its most simplified form like this:

Example 2
Find 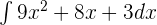
Solution
First, we will break down the integrals using addition/subtraction or multiplication by constants. Hence, we can write the above function like this:

Now, we will shift the constants before the integral sign like this:

Now, we will apply the power rule 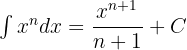 to find the integrals of the powers and integral constant rule to calculate the integral of the last term of the above polynomial:
to find the integrals of the powers and integral constant rule to calculate the integral of the last term of the above polynomial:
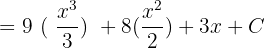
In the last step, write the final answer in its most simplified form like this:
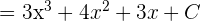
Example 3
Find 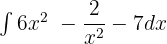
Solution
First, we will break down the integrals using addition/subtraction or multiplication by constants. Hence, we can write the above function like this:
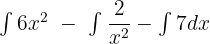
Now, we will shift the constants before the integral sign like this:
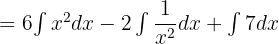
Now, we will apply the power rule 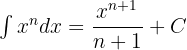 to find the integrals of the powers and integral constant rule to calculate the integral of the last term of the above polynomial:
to find the integrals of the powers and integral constant rule to calculate the integral of the last term of the above polynomial:
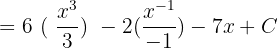
In the last step, write the final answer in its most simplified form like this:
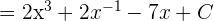
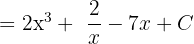
Example 4
Find 
Solution
First, we will break down the integrals using addition/subtraction or multiplication by constants. Hence, we can write the above function like this:
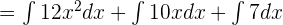
Now, we will shift the constants before the integral sign like this:

Now, we will apply the power rule 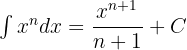 to find the integrals of the powers and integral constant rule to calculate the integral of the last term of the above polynomial:
to find the integrals of the powers and integral constant rule to calculate the integral of the last term of the above polynomial:
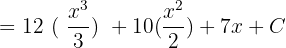
In the last step, write the final answer in its most simplified form like this:

Example 5
Find 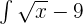
Solution
Remember that  can be written in exponential form as
can be written in exponential form as 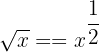 . Hence, we can write the function like this:
. Hence, we can write the function like this:
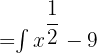
In the next section, we will apply the power rule 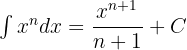 like this:
like this:
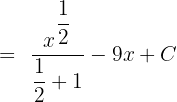
Simplify the above expression to get the final answer:
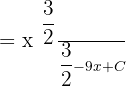
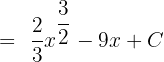
We can also write the answer in exponential form like this:
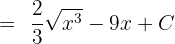
Example 6
Find 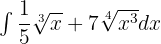
Solution
Write the function in exponential form like this:
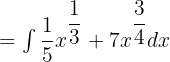
Break down the above function by using the integral sign with both the terms as shown below:
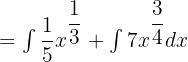
Use the power rule 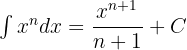 to integrate the function like this:
to integrate the function like this:
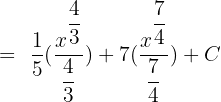
Simplify the above expression to get the final answer:
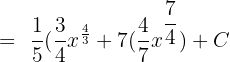
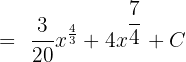
We can write the answer in exponential form like this:
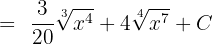
Example 7
Find 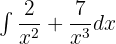
Solution
We can rewrite the above expression in terms of exponents like this:
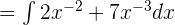
Rewrite the above expression again using the integration sign with both the terms:

In the next step, apply the power rule 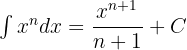 to find the integral of the function like this:
to find the integral of the function like this:

Simplify the above expression to write the final answer:
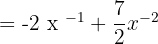
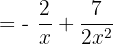













Hi,
what is the integral of ;
(k ^ -u x e ^ u)
Thanks,