Solve the following integrals:
Exercise 1
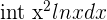
Exercise 2
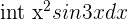
Exercise 3
Exercise 4
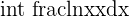
Exercise 5
Exercise 6
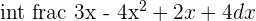
Exercise 7
Exercise 8
Exercise 9
Exercise 10
Exercise 11
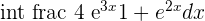
Exercise 12
Solution of exercise 1
,
,
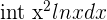
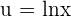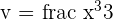
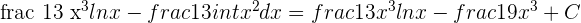
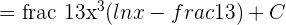
Solution of exercise 2
,
,
,
,
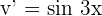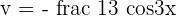
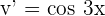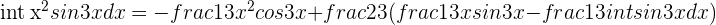
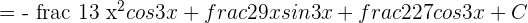
Solution of exercise 3
,
,
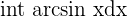
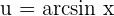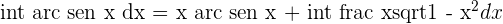
Solution of exercise 4
,
,
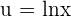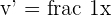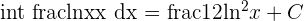
Solution of exercise 5
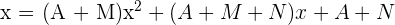
Equal the coefficients of the two members.
0 = A + M 1 = A + M + N 0 = A + N A = -1, M = 1, N = 1
The first integral is of logarithmic type and the second has to be broken in two.
Multiply by 2 in the second integral.
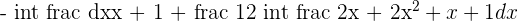
The 2 in the numerator of the second integral transforms into 1 + 1.
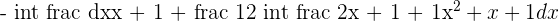
Decompose the second integral into two others.
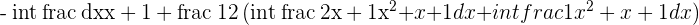
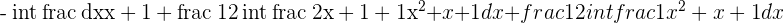
Solve the first two integrals.
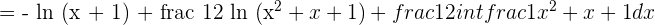
Transform the denominator of a squared binomial.
Multiply the numerator and denominator by 4/3, to obtain one in the denominator.
Under the squared binomial, multiply by the square root of 4/3.
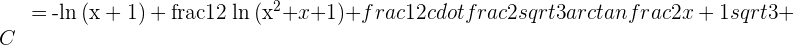
Solution of exercise 6
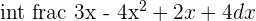
Add and subtract 3 in the numerator, decompose into two fractions and in the first one remove common factor 3.
Multiply and divide in the first fraction by 2.
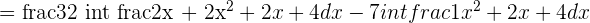
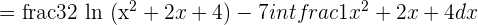
Transform the denominator of a squared binomial.
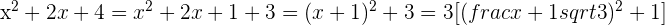
Realize a change of variable.
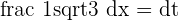
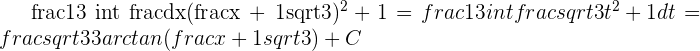
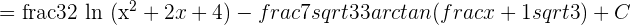
Solution of exercise 7
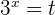
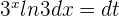
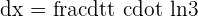
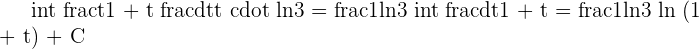
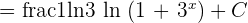
Solution of exercise 8
,
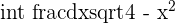
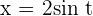
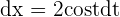
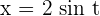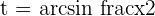
Solution of exercise 9
,
,
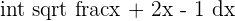
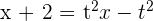
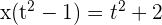
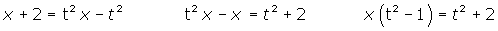
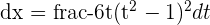
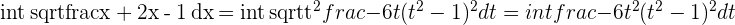
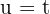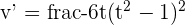Make the second integral.
,
,
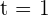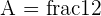
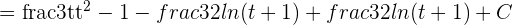
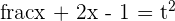
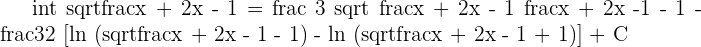
Solution of exercise 10
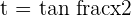
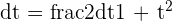
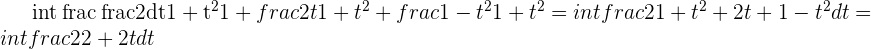
Solution of exercise 11
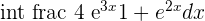
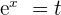
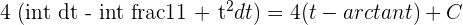
Solution of exercise 12
,
Summarise with AI:
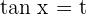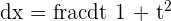
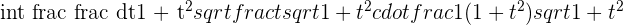
Did you like this article? Rate it!
Loading...
