Chapters

What is Integration?
When you need to find the area of a shape, you usually use a formula for it. For example, below we have a triangle.

In order to find the area of the triangle, you can simply plug in the height and the length of the base into the following formula.

This gives us the exact area of the triangle. Many shapes have formulas for their areas, take a look at some examples below.
| Shape | Area Formula | Dimensions |
| Circle |  | r = radius |
| Square | 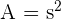 | s = side |
| Rectangle | 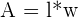 | l = length w = width |
Now, what if we plot the triangle from our example above onto a graph. Can you guess what the area is?

The truth is that the area would be the same. This makes sense, it’s the same triangle after all! So how do we find the area? Well, simple, we would still use the formula for the area of a triangle. The only difference is that instead of being given the measurements of the triangle, perhaps we’re only given points.
So, if this is true for all shapes, what if we don’t have a standard shape at all? What if, instead, we want to find the area of something like this:

This is where integration comes in. When we have any equation for any line, we can use that equation to derive a formula for the area of that line. This is what integration is: it takes an equation as an input and gives you a different equation as an output that is actually just an area formula.

| What | Description | Example | |
| A | Integral sign | The m and n are the upper and lower bounds, which is the interval we want to find the area for |  |
| B | Function | Any function that we want to find the area for |  |
| C | dx | This term specifies the variable we are integrating | 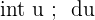 |
You can also think of integration as the opposite of taking the derivative. Compare the processes below.
| Function | Derivative | Integral | |
| Notation | f(x) | f’(x) |  |
| Rule | Any function | 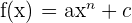
| 
|
| Example | f(x) = x^{2} | f’(x) = 2x^{2-1} = 2x | 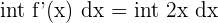 = =
|
What are Trigonometric Functions?
Let’s continue with the idea of triangles. Trigonometry is actually based on triangles - which is helpful, because their behaviour (like areas) is very predictable. We usually use right triangles in trigonometry.

Remember, adjacent refers to the fact that this side is adjacent, or next to, the angle  . Opposite means it’s the side opposite the angle. This is a summary of the behaviour of triangles when it comes to the lengths of their sides:
. Opposite means it’s the side opposite the angle. This is a summary of the behaviour of triangles when it comes to the lengths of their sides:
| Sine | 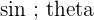 = = | Sin of the angle is = | 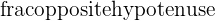 |
| Cosine | 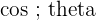 = = | Cos of the angle is = |  |
| Tangent | 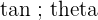 = = | Tan of the angle is = |  |
Why is this useful? Take a simple example: a travel company wants to make a new route, which is highlighted below.
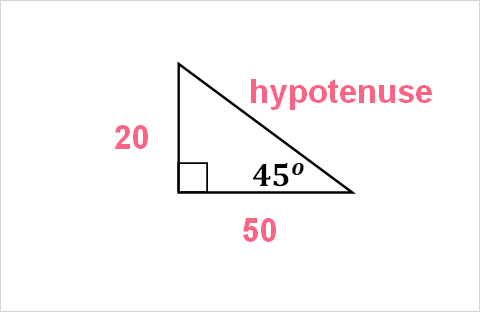
They know the distance between island A and B, as well as the distance between island B and C. Instead of spending a lot of time, money and effort to measure this distance physically, they can use the properties of triangles to calculate the distance between island A and C.
| Step 1 | Step 2 | Step 3 |
| cos(45) = 50/hypotenuse | hyp = 50/cos(45) | hyp = 95 |
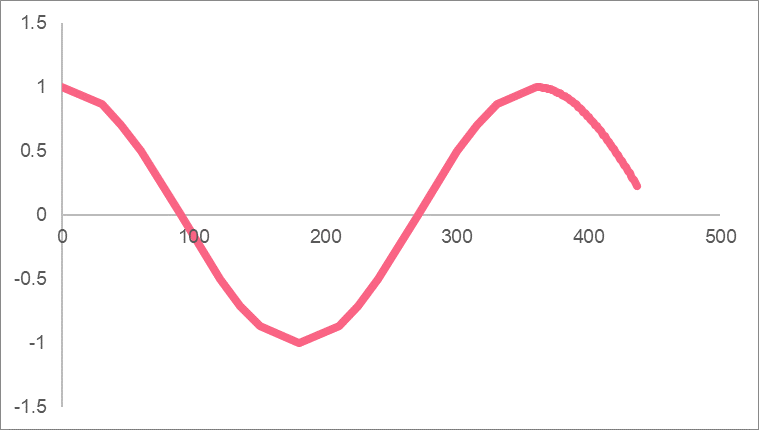
What happens when we plot trigonometric functions though? Take a look at the cosine graph:

So how do we get a graph like that from a triangle? Let's take the cosine of 4 values.
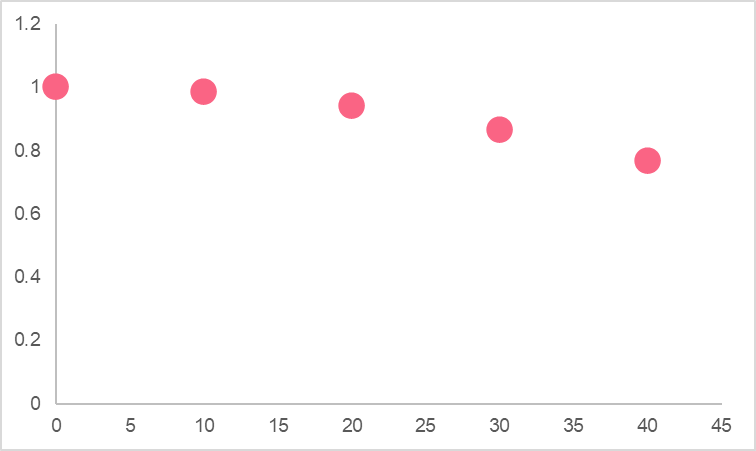
| A | B | C | D | E |
| (0,1) | (10, 0.985) | (20, 0.94) | (30, 0.866) | (40, 0.766) |
As you can see, we end up with 4 different triangles. However, the value of the cosine starts to create a line. If we continue this and take the cosine of more values, we end up with a graph like this.
You can also think about the cosine and sine corresponding to any angle as x and y coordinates. Like we did in the previous example, we can plot 5 triangles with the following coordinates.

| A | B | C | D | E | |
Angle 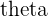 (Degrees) (Degrees) | 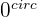 | 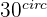 | 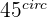 | 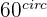 |  |
Cos(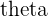 ) ) | 1 | 0.87 | 0.71 | 0.5 | 0 |
Sin(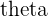 ) ) | 0 | 0.5 | 0.71 | 0.87 | 1 |
If we do this for all angles between 0-360 degrees, we get a circle:

This is known as the unit circle.
Integration Rules for Trigonometric Functions
When integrating trig functions, it’s really easy. You simply need to follow these rules.
| Integration Function | Result | Example | |
| Cosine |  | sin(x) | 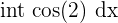 = sin(2) = sin(2) |
| Sine |  | -cos(x) | 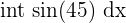 = -cos(45) = -cos(45) |
| Tangent |  | tan(x) | 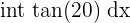 = tan(20) = tan(20) |
What is an Inverse?
An inverse function undoes a function. Let’s take a look an example.
| Notation | Example | Description | |
| Function | f(x) | 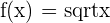 | The function is the square root of any number x |
| Inverse Function | 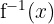 | 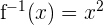 | The inverse of the function ‘undoes’ the square root by taking the square of x |
How do you find a function’s inverse? Normally, you follow these steps.
| 1 | Start with a function and replace f(x) with y | 
|
| 2 | Swap y and x | 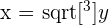 |
| 3 | Solve for y | 
|
Inverse of Trigonometric Function
How do you get the inverse of a trig function? The first two steps are the same.

| A | Start with a trig function and replace f(x) with y |
| B | Swap x and y |
Now, to solve for y, you have to take the ‘inverse sine’ of y, which cancels out the sine operation.

| C | Take the inverse trig function of both sides to get the inverse function |
There are a couple of differences between a sine and inverse sine function.

| Sine | Inverse Sine |
| x is an angle | x is a sine value |
| y gives us the corresponding sine value | y gives us the corresponding angle |
The inverse of a trig function can also be written like the following.












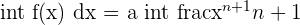
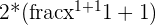 =
=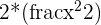

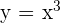



Hi,
what is the integral of ;
(k ^ -u x e ^ u)
Thanks,