Integration is a reverse process of differentiation, hence we can also call it as inverse differentiation. It is a technique of finding a function with its derivative. In this article, we have jotted down some basic integration formulas. We will also solve some examples using these formulas.
Integration Formulas
Some basic integration formulas are given below: 1.
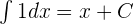
2.
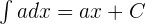
3.
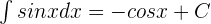
4.
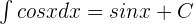
5.
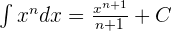, where
6.
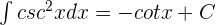
7.
8.
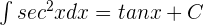
9.
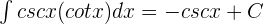
10.
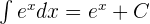
11.
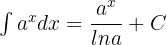, where
, and
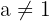
12.
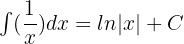
Now, we will see how to use the above formulas to find the integrals.
Example 1
Find the integral of the following function:
Solution
Since the above function contains power or exponent, hence we will use the following formula to compute the integral:
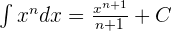, where
In this question, n = 6. Now, we will put this value in the above formula:
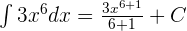
Simplifying the above equation will give us the following answer:
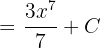
Example 2
Find the integral of the following function:
Solution
Since the above function contains variables with exponents and constant both, hence we will use the following formulas to compute the integral:
For exponent: 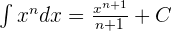, where
For constant: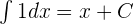
But before applying these formulas, we will rewrite the question using integration sum rule like this:
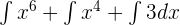
We will separately integrate the three terms like this:
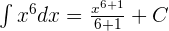
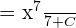
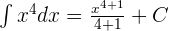
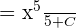
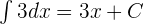
Now, we will combine these answers again to write the integral of the entire function:
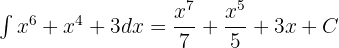
Example 3
Find the integral of the following function:
Solution
Using the integration sum rule, we can rewrite the above function like this:
We will treat both the terms as separate functions for now. We know that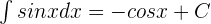
and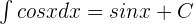
.
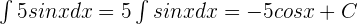
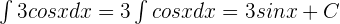
Combining the integrals of both the terms will give us the following answer:
Example 4
Find the integral of the following function:
Solution
First, we will convert this radical function into exponential form like this:
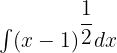
Now, we will use substitution method to solve the problem. Suppose (x - 1) = u. This means that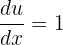
and du= dx. Substituting these values in the above equation will give us the following expression:
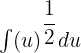
Now, we will use the formula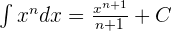
, where
to find the integral:
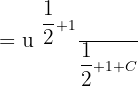
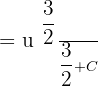
In the end, we will substitute u = x - 1, again in the above expression to get the final answer:
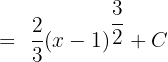
Example 4
Find the integral of the following function:
Solution
First, we will rewrite the above example by using sum rule of integration like this:
It means that we will integrate the three terms separately. Let us first integrate the first term. To do so, we will convert this radical function into exponential form like this:
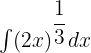
Now, we will use substitution method to find the integral of this term. Suppose 2x = u. This means that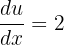
and
. We can easily find the value of dx which is equal to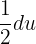
. Substituting these values in the above equation will give us the following expression:
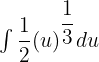
Move the fraction before the integral sign like this:
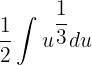
Now, we will use the formula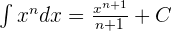
, where
to find the integral:
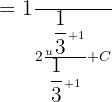
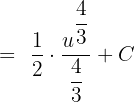
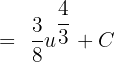
In the end, we will substitute u = 2x again in the above expression to get the final integral of this term:
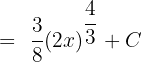
Now, we will integrate the remaining two terms. We will use the formula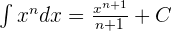
, where
again to find the integral of the second term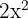
.
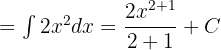
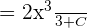
The third term is a constant, so we will use the formula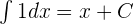
to integrate it.
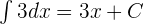
In the end, we will combine the integrals of all the three terms to write the final answer as shown below:
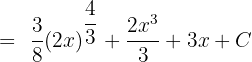
Example 5
Find the integral of the following function:
Solution
The question in this example is an exponential function. Hence, we will use the formula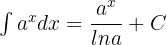
, where
, and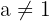
to integrate it.
= 
= 
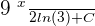
Example 6
Find the integral of the following function:
Solution
In this problem, we will use the substitution method to find the integral. Suppose 5x - 2 = u. If u = 5x - 2, then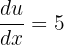
. From this, we can calculate du and dx.
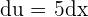
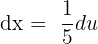
Now, we will substitute these values in the above function like this:
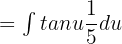
Move the fraction before the integral sign like this:
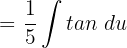
Now, we will use the formula
. Substituting these values in the above function will give us the final answer:
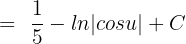
Substitute u = 5x - 2 again in the above expression to get the following answer:
Summarise with AI:
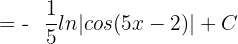
Did you like this article? Rate it!
Loading...
